Pythonで関数のグラフを描く

数学の具体的な計算にPythonを使って、数学もPythonも同時に学んでしまいましょう。今回はPythonを使って関数のグラフを作成してみたいと思います。動作の確認はJupyterNotebookを用いた場合で行っています。インターフェイスなどの動作環境の違いによって適宜変更点があるかもしれません。

Pythonを使った数式の処理については以下の過去記事にまとめています。あわせて読んでみてください：

pianofisica.hatenablog.com

多項式関数の描画
指数関数の描画
三角関数の描画
自分で定義した関数（Heaviside関数）の描画
自分で定義した関数の描画
詳細設定

多項式関数の描画

例として５次の多項式関数

$\quad\displaystyle{f(x)=x^5+x^4-10x^3+2x-8}$

をグラフに描いてみます：

import matplotlib.pyplot as plt
import numpy as np
p = np.linspace( -4, 3, 70)   # linspace(min, max, N) で範囲 min から max を N 分割します
q = p**5+p**4-10*p**3+2*p-8
plt.plot(p, q)
plt.show()

から

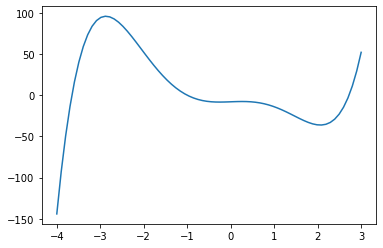
というグラフが作成されます。

この描画の方法では、プロット範囲の分割点での関数値を直線でつないでいるので、分割数を小さくとってしまうと作成されるグラフはガタガタになってしまうことに注意が必要です：

import matplotlib.pyplot as plt
import numpy as np
p = np.linspace( -4, 3, 8)
q = p**5+p**4-10*p**3+2*p-8
plt.plot(p, q)
plt.show()

指数関数の描画

変域の下端と上端、分割数を linspace 内に具体的に書き込むのではなく、変数（ xmin, xmax, N など）としておいて数値を格納させるように書いたほうが、より視認性も汎用性も高くて便利だと思います。

import matplotlib.pyplot as plt
import numpy as np
N = 300
xmin = -3
xmax = 3
p = np.linspace( xmin, xmax, N)
q = np.exp(-p)
plt.plot(p, q)
plt.show()

三角関数の描画

さらに、描きたい関数も具体形を直接書くのではなく、別で定義しておいたほうが、より一般化しやすいでしょう：

import matplotlib.pyplot as plt
import numpy as np
N = 100
xmin = -10
xmax = 10
def f(x):
   return np.sin(x)
p = np.linspace( xmin, xmax, N)
q = f(p)
plt.plot(p ,q)
plt.show()

自分で定義した関数（Heaviside関数）の描画

Heaviside関数（階段関数、ステップ関数）は

$\quad\displaystyle{H(x)=\begin{cases} \ 0 \quad (x<0)\\ \ 1 \quad ({\rm otherwise}) \end{cases}}$

で定義されます。この関数をPythonで自分で定義し、グラフに描いてみます：

import matplotlib.pyplot as plt
import numpy as np
N = 60
xmin = -3
xmax = 3
def f(x):
   if x < 0: return 0
   else: return 1
p = np.linspace( xmin, xmax, N)
plt.plot( p, [f(p[k]) for k in range(N)] )
plt.show()

自分で定義した関数の描画

上でHeaviside関数を定義したときのPythonの書法のちょっとした応用として、実軸上の正の領域と負の領域で異なる関数形を持つような場合を考えてみます：

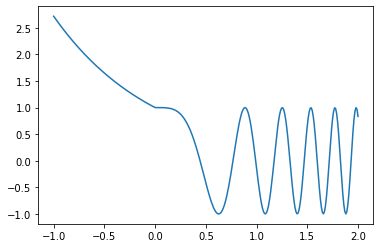
$\quad\displaystyle{f(x)=\begin{cases} \ e^{-x} \quad &(x\leq 0)\\ \ \cos(8x^2) \quad &({\rm otherwise}) \end{cases}}$

この関数をPythonで自分で定義し、グラフに描いてみます：

import matplotlib.pyplot as plt
import numpy as np
N = 300
xmin = -1
xmax = 2
def f(x):
   if x <= 0: return np.exp(-x)
   else: return np.cos(8*x**2)
p = np.linspace( xmin, xmax, N)
plt.plot( p, [f(p[k]) for k in range(N)] )
plt.show()