Pythonで学ぶ1次元振動の数値解(フックの法則から戸田ポテンシャルへ)
数学・物理学の具体的な計算にPythonを使って、数学・物理学もPythonも同時に学んでしまいましょう。今回はPythonを使って、振動を表す運動方程式(2階常微分方程式)の解を数値的に求めてみたいと思います。最初にもっとも基本的な調和振動子を考え、徐々にそこから外れた場合について考察を進めてみます。
本記事は以下の記事の続編的な位置付けになります。あわせて読んでみてください:
pianofisica.hatenablog.com
pianofisica.hatenablog.com
1次元調和振動子(復元力:変位の1次)
バネの振動などはフックの法則(復元力は平衡点からの変位に比例する)によって記述されます。そのような物理系を1次元調和振動子といい、その運動方程式は以下で与えられます:
この一般解が三角関数で与えられることは高校物理でもおなじみでしょう。あるいは解析計算のライブラリであるSymPyを使えば
import sympy as sp sp.init_printing() sp.var('x') y = sp.Function('y')(x) eq1 = sp.Eq( sp.diff(y,x,2), -y ) sp.dsolve(eq1)
から、一般解
を得ます。ですが、ここではあえてこの物理系を数値的に解析してみます。というのは、よく知られた系を数値的に調べ解析的な解と見比べてみることで、数値計算の手法がうまくいっているがどうかテストするためです。
数値的に扱いやすくするために、まず方程式を1階化した方程式系に書き直します:
Taylor展開の2次の補正まで考慮します(Runge-Kutta法):
これらから差分方程式
を得ます。ただし、 としました。初期条件
のもとで、この差分方程式をPythonで数値的に計算してみましょう:
N = 3000 # ステップ数 h = 0.01 # 差分間隔 X = [0] # 時刻の原点 Y1 = [1] # 初期位置 P1 = [0] # 初期速度 # 差分方程式 def x(k): return h+X[k-1] def y1(k): return Y1[k-1]+h*(P1[k-1])+h**2/2*(-Y1[k-1]) def p1(k): return P1[k-1]+h*(-Y1[k-1])+h**2/2*(-P1[k-1]) # 各ステップにおける時刻・位置・速度データの格納 for k in range(N): X.append( x(k+1) ) Y1.append( y1(k+1) ) P1.append( p1(k+1) ) import matplotlib.pyplot as plt # 時刻・位置データの表示 plt.plot(X, Y1) plt.show()
から得られるのが次の図です:
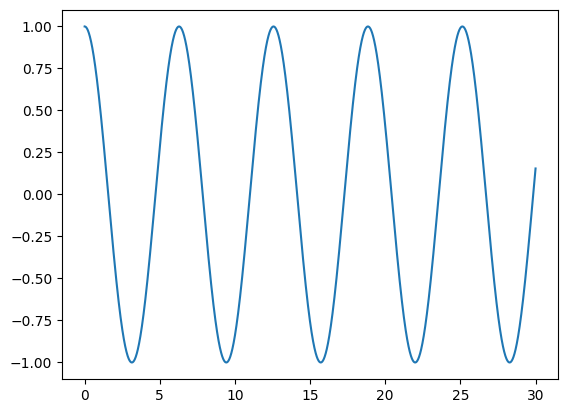
ここで横軸は時刻、縦軸は質点の位置です。解析解 とよく一致します。よって、この計算方法がうまくいっていることが確認できます。
非線形な振動子(復元力:変位の3次)
復元力が平衡点からの変位の3次で与えられる、次のような非線形な運動方程式
を考えてみましょう。方程式の解が単純な三角関数の線型結合ではないことはすぐにわかります。実際
import sympy as sp sp.init_printing() sp.var('x') y = sp.Function('y')(x) eq2 = sp.Eq( sp.diff(y,x,2), -y**3/6 ) sp.dsolve(eq2)
から、解析的な解は
となり、もはや初等関数では書き表せないことがわかります。このような場合には数値計算が力を発揮します。数値計算のために調和振動子と同様、まず方程式を1階化します:
ここでもTaylor展開の2次の補正まで考慮します(Runge-Kutta法):
これらから差分方程式
を得ます。ただし、 としました。初期条件
のもとで、これらをPythonに入力して計算してみます:
N = 3000 h = 0.01 X = [0] Y2 = [1] P2 = [0] def x(k): return h+X[k-1] def y2(k): return Y2[k-1]+h*(P2[k-1])+h**2/2*(-Y2[k-1]**3/6) def p2(k): return P2[k-1]+h*(-Y2[k-1]**3/6)+h**2/2*(-3*Y2[k-1]**2/6*P2[k-1]) for k in range(N): X.append( x(k+1) ) Y2.append( y2(k+1) ) P2.append( p2(k+1) ) import matplotlib.pyplot as plt plt.plot(X, Y1) plt.plot(X, Y2) plt.show()
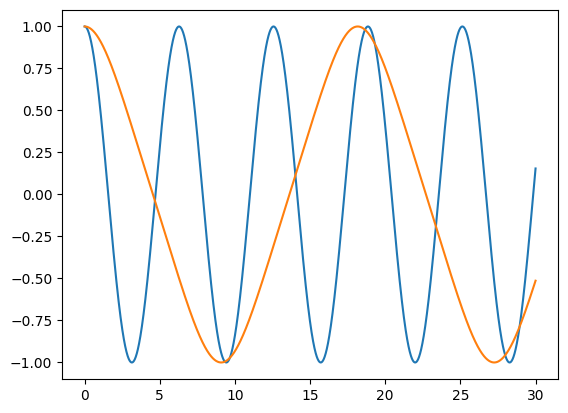
ここで青線が調和振動子(1次)、オレンジ線が非線形振動子(3次)の場合です。調和振動子の場合と比べればゆっくりとですが、3次の復元力の場合にもやはり振動することがわかります。このことは定性的にも理解できます。というのは、いま変位として を考えているので
が常に成り立ち、調和振動子のほうがより大きな復元力を発揮しているからです。
非線形な振動子(復元力:変位の1次+3次)
上でみた2つの例を組み合わせてみましょう:
初期条件 のもとで、これらをPythonに入力して計算してみます:
N = 3000 h = 0.01 X = [0] Y3 = [1] P3 = [0] def x(k): return h+X[k-1] def y3(k): return Y3[k-1]+h*(P3[k-1])+h**2/2*(-Y3[k-1]-Y3[k-1]**3/6) def p3(k): return P3[k-1]+h*(-Y3[k-1]-Y3[k-1]**3/6)+h**2/2*(-P3[k-1]-3*Y3[k-1]**2/6*P3[k-1]) for k in range(N): X.append( x(k+1) ) Y3.append( y3(k+1) ) P3.append( p3(k+1) ) import matplotlib.pyplot as plt plt.plot(X, Y1) plt.plot(X, Y2) plt.plot(X, Y3) plt.show()
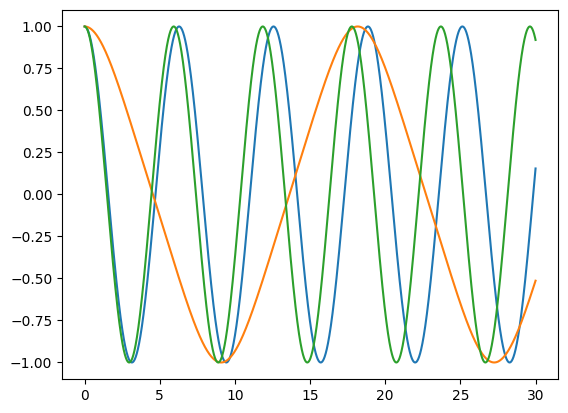
ここで青線が調和振動子(1次)、オレンジ線が非線形振動子(3次)、緑線が(1次+3次)の場合です。線形の復元力に3次の項が加わったことで、振動の周期が少し短くなったことがわかります。
非線形な振動子(復元力:変位の双曲線関数、戸田ポテンシャル)
ここまで見た例では、変位の3次の項には意味ありげな数因子( )を乗じていました。これは
の最初の2項と一致させるようにあらかじめ選んでおいたものです。ここで双曲線関数による次のような復元力を考えてみます:
初期条件 のもとで、これらをPythonに入力して計算してみます:
import numpy as np N = 3000 h = 0.01 X = [0] Y4 = [1] P4 = [0] def x(k): return h+X[k-1] def y4(k): return Y4[k-1]+h*(P4[k-1])+h**2/2*(-np.sinh(Y4[k-1])) def p4(k): return P4[k-1]+h*(-np.sinh(Y4[k-1]))+h**2/2*(-np.cosh(Y4[k-1]))*P4[k-1] for k in range(N): X.append( x(k+1) ) Y4.append( y4(k+1) ) P4.append( p4(k+1) ) import matplotlib.pyplot as plt plt.plot(X, Y1) plt.plot(X, Y2) plt.plot(X, Y3) plt.plot(X, Y4) plt.show()
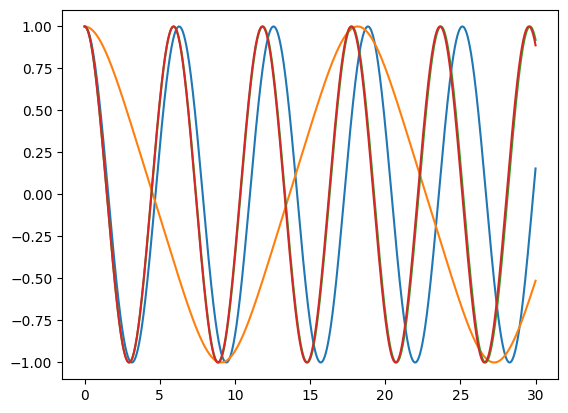
ここで青線が調和振動子(1次)、オレンジ線が非線形振動子(3次)、緑線が(1次+3次)、赤線が双曲線関数による復元力の場合です。双曲線関数は無限次数の項まで含むわけですが、数因子の抑制によって(1次+3次)の場合に補正が加わったような結果になりました。
多くの場合、微分方程式の解は具体的な関数として解析的に書き表すことはできません。しかし数値的に解を求めることによって系の性質を調べることができます。本記事では振動子を例にとって一連の考察をしてみました。
ちなみに最後に考察した双曲線関数による復元力を導くポテンシャル
を求めてみると
と書けることがわかります。この関数系 で与えられる非線形相互作用のポテンシャルは『戸田ポテンシャル』と呼ばれ、ソリトン理論につながる重要な対象です。