Maximaで学ぶ常微分方程式の数値解

数学の具体的な計算にMaximaを使って、数学もMaximaも同時に学んでしまいましょう。今回はMaximaを使って、常微分方程式の解を数値的に求めてみたいと思います。本記事で記載している図の描画の確認は、wxMaxima上でgnuplotを用いた場合で行っています。インターフェイスなどの動作環境の違いによって適宜変更点があるかもしれません。

常微分方程式

常微分方程式

一般に、未知関数とその導関数を含んだ方程式を微分方程式といいます。一変数関数の場合を常微分方程式、多変数関数の場合を偏微分方程式と呼びます。Maximaに実装されているコマンドを使って、力学で現れる具体的な常微分方程式をいくつか解析的に解いているのが次の記事です：

pianofisica.hatenablog.com

本記事では、必ずしも解析的な解が得られない場合も多いことから、初期条件から数値的に常微分方程式の解を求める方法をみていきます。

Euler法（オイラー法）

１階常微分方程式

$\quad \displaystyle{\frac{dy}{dx}=f(y)}$

を考えましょう。微分の定義から、微小変位 $\Delta x$ に対して

$\quad \displaystyle{\frac{y(x+\Delta x)-y(x)}{\Delta x}\sim f(y(x))+\mathcal{O}(\Delta x^2)}$

が成り立ちます。そこで $h$ を微小な差分間隔として

$\quad \displaystyle{ y(x_{n+1}) = y(x_{n})+h\,f(y(x_{n})) }$

によって各 $x_n=x_0+nh \ (n=0,1,\dots,N)$ での $y$ の値を求めることができます。

具体例として $f(y)=-y$ として

$\quad \displaystyle{\frac{dy}{dx}=-y}$

という微分方程式を考えてみます。この微分方程式の一般解は $y=Ce^{-x}$ で与えられますが、数値的な計算が解析的な解とどれほど違ってくるかを体験してみましょう。初期条件として $C=20$ の場合、差分間隔を $h=0.1$ として計算してみます：

kill(all)$ h:0.1$ N:60$
y[0]:20$
n:0$ while n<N+1 do(
y[n+1]:y[n]+h*(-y[n]),
n:n+1)$
L:makelist([n*h, y[n]],n,0,N)$
T(x):=20*exp(-x)$
plot2d ([[discrete, L],T(x)],[x, 0, h*N],[style,points,lines],
[xlabel, "number of steps"],[ylabel, "value of y"]);

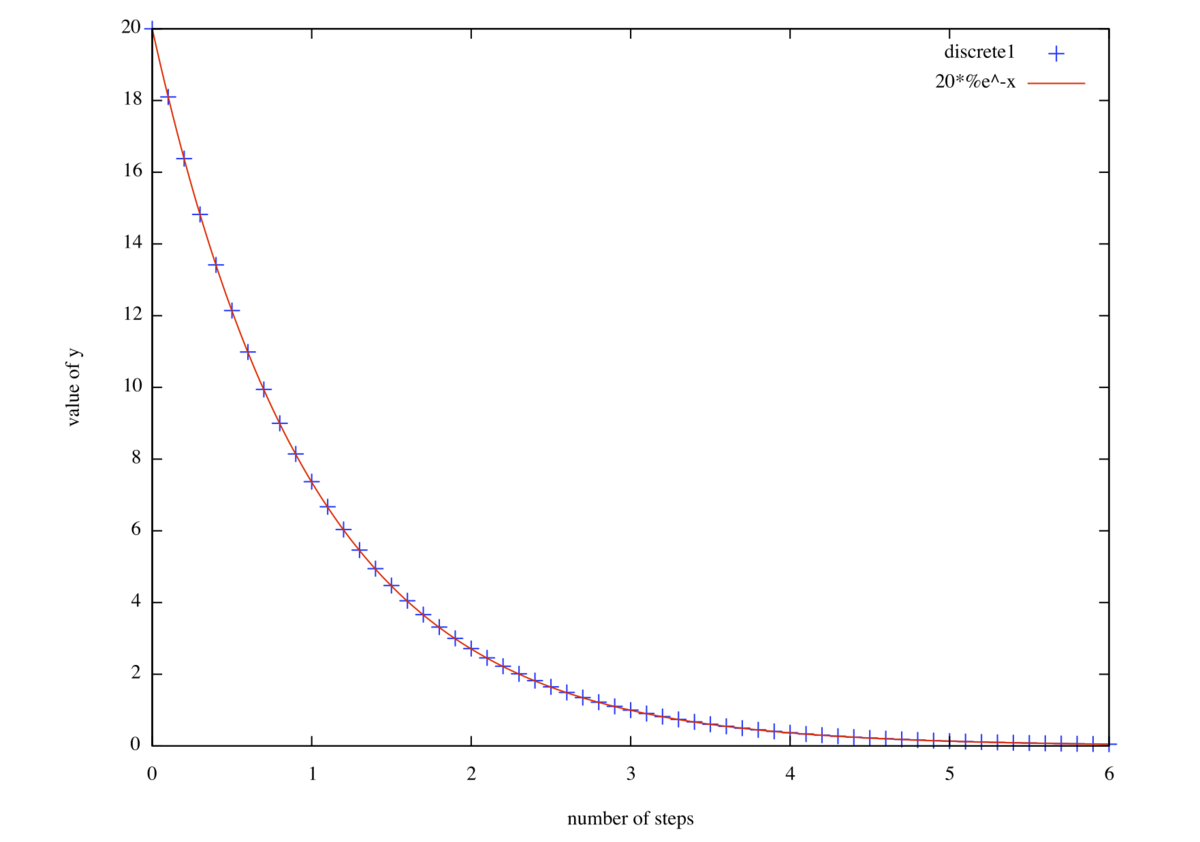
によって得られるのが次のグラフです：

f:id:pianofisica:20200914163529p:plain

青い印が数値的に求めた値で、赤線が解析的な解です。定性的には解の様子をうまく表していますが、あまり精度が良いようには見えません。

改良Euler法（Runge-Kutta法：ルンゲ=クッタ法）

差分間隔を保ったまま、評価点の個数も変えずに、計算の精度を上げるにはどのようにすれば良いでしょうか？ここでTaylor展開の公式から、微小な差分間隔 $h$ に対して

$\quad \displaystyle{\begin{aligned}y(x_{n+1})&\sim y(x_n)+h\,f(y(x_n))+\frac{h^2}{2}\,y''(x_n)\\&\sim y(x_n)+h\,f(y(x_n))+\frac{h^2}{2}\,f'(y)\,f(y(x_n))\end{aligned}}$

と近似されることを使って

kill(all)$ h:0.1$ N:60$
y[0]:20$
n:0$ while n<N+1 do(
y[n+1]:y[n]+h*(-y[n])+h^2/2*(-1)*(-y[n]),
n:n+1)$
L:makelist([n*h, y[n]],n,0,N)$
T(x):=20*exp(-x)$
plot2d ([[discrete, L],T(x)],[x, 0, h*N],[style,points,lines],
[xlabel, "number of steps"],[ylabel, "value of y"]);

から得られるのが次の図です：

f:id:pianofisica:20200914164404p:plain

解析的な解の曲線とかなり一致し、近似が改良されていることがわかります。

裳華房の『数値計算』（柳田・中木・三村）では、数値計算の基本的な手法を紹介しています：

<br />

常微分方程式を数値的にいかにして解くかを数学的背景を基礎に解説していて、原理の面から理解したいという人にはうってつけの本だと思います。

２階常微分方程式

運動方程式にみられるように、２階微分方程式

$\quad \displaystyle{\frac{d^2y}{dx^2}=f\left(y,\frac{dy}{dx}\right)}$

は応用上の重要な対象です。これを上のようにして数値的に解析したいわけですが、そのために連立方程式による１階化

$\quad \displaystyle{\frac{dy}{dx}=p\qquad\qquad\frac{dp}{dx}=f\left(y,p\right)}$

を考えます。この連立微分方程式から得られる近似の関係式

$\quad \displaystyle{\begin{aligned} y(x+h) &=y(x)+hp(x)+\frac{h^2}{2}p'(x)+\dots\\ &=y(x)+hp(x)+\frac{h^2}{2}f(y,p)+\dots \\ p(x+h) &=p(x)+hf\left(y,p\right) +\frac{h^2}{2}\left(p\frac{\partial f(y,p)}{\partial y}+f\frac{\partial f(y,p)}{\partial p}\right) +\dots \end{aligned}}$

を用いて上と同様の計算ができます。

もう少し具体的に詳しくみるために単振動の運動方程式

$\quad \displaystyle{\frac{d^2y}{dx^2}=-y}$

を考えましょう。いま連立微分方程式によって線形化して

$\quad \displaystyle{\frac{dy}{dx}=p \qquad\qquad \frac{dp}{dx}=-y}$

です。初期条件として $y(0)=1,\ p(0)=0$ としましょう。Euler法で計算すると

kill(all)$ h:0.01$ N:10000$
y[0]:1$ p[0]:0$
n:0$ while n<N+1 do(
y[n+1]:y[n]+h*(p[n]),
p[n+1]:p[n]+h*(-y[n]),
n:n+1)$
L:makelist([n*h, y[n]],n,0,N)$
T(x):=cos(x)$
plot2d ([[discrete, L],T(x)],[x, 0, h*N],[style,lines,lines],
[xlabel, "number of steps"],[ylabel, "value of y"]);

から得られるのが次の図です：

f:id:pianofisica:20200915165056p:plain

青線は数値計算によって得られる解、赤線が解析解 $y(x)=\cos(x)$ です。数値解は、周期は一致しますが、振幅が徐々に大きくなってしまっていることがわかります。

２次の補正まで入れて（Runge-Kutta法で）計算したのが以下です：

kill(all)$ h:0.01$ N:10000$
y[0]:1$ p[0]:0$
n:0$ while n<N+1 do(
y[n+1]:y[n]+h*(p[n])+h^2/2*(-y[n]),
p[n+1]:p[n]+h*(-y[n])+h^2/2*(-p[n]),
n:n+1)$
L:makelist([n*h, y[n]],n,0,N)$
T(x):=cos(x)$
plot2d ([[discrete, L],T(x)],[x, 0, h*N],[style,lines,lines],
[xlabel, "number of steps"],[ylabel, "value of y"]);