Pythonの条件分岐

数学の具体的な計算にPythonを使って、数学もPythonも同時に学んでしまいましょう。今回はPythonの条件分岐を使って、KroneckerのデルタやHeavisideの階段関数を定義する方法をみたいと思います。本記事で記載している図の描画の確認は、JupyterNotebook上で行っています。インターフェイスなどの動作環境の違いによって適宜変更点があるかもしれません。

条件分岐

条件分岐

Pythonの条件分岐の例について備忘録的にまとめました。

if - else

==（等しいとき）

引数が０に等しいときのみ１を返し、それ以外の値では０を返すような関数を定義します：

def d(x):
   if x == 0: return 1
   else: return 0

とすると、関数の引数に具体的に数を代入して、たとえば

[ d(-2), d(-1), d(0), d(1), d(2)]

から

$\qquad\displaystyle{d(-2)=0,\quad d(-1)=0,\quad d(0)=1,\quad d(1)=0,\quad d(2)=0}$

となります。以下の例では、この関数 $d(x)$ の条件部分である『==』を適当に変えて新たな関数を定義し、関数の引数に数を代入しています。

!=（等しくないとき）

def d1(x):
   if x != 0: return 1  # 上でみた関数の例で == としていたところを != に変えました
   else: return 0
[ d1(-2), d1(-1), d1(0), d1(1), d1(2)]

<=（以下のとき）

def d2(x):
   if x <= 0: return 1
   else: return 0
[ d2(-2), d2(-1), d2(0), d2(1), d2(2)]

<（未満のとき）

def d3(x):
   if x < 0: return 1
   else: return 0
[ d3(-2), d3(-1), d3(0), d3(1), d3(2)]

>（上回るとき）

def d4(x):
   if x > 0: return 1
   else: return 0
[ d4(-2), d4(-1), d4(0), d4(1), d4(2)]

>=（以上のとき）

def d5(x):
   if x >= 0: return 1
   else: return 0
[ d5(-2), d5(-1), d5(0), d5(1), d5(2)]

Kroneckerのデルタ

Kroneckerのデルタは整数を引数として

$\qquad\displaystyle{\delta_{m,n}=\left\{\begin{array}{ll} \ 1 & (m=n) \\ \ 0 & \text {(otherwise)}\end{array}\right.}$

で定義されます。これをPythonで実現するには条件式を使って以下のようにします：

def kd(m,n):
   if m == n: return 1
   else: return 0
[ kd(-2,0), kd(-1,0), kd(0,0), kd(1,0), kd(2,0), kd(2,2)]

Heaviside関数（階段関数、ステップ関数）

Heaviside関数は実軸上

$\qquad\displaystyle{H(x)=\left\{\begin{array}{ll} \ 0 & (x<0) \\ \ 1 & \text {(otherwise)}\end{array}\right.}$

と定義されます。これをPythonで自分で定義し、グラフに描いてみます：

import matplotlib.pyplot as plt
import numpy as np
N = 40
xmin = -2
xmax = 2
def H(x):
   if x < 0: return 0
   else: return 1
p = np.linspace( xmin, xmax, N)
plt.plot( p, [H(p[k]) for k in range(N)] )
plt.show()

f:id:pianofisica:20200928144946p:plain

not

Heaviside関数のヴァリエーションとして

$\qquad\displaystyle{H_0(x)=\left\{\begin{array}{ll} \ 1 & (x<0) \\ \ 0 & \text {(otherwise)}\end{array}\right.}$

という関数を考えてみましょう。これは上で使った定義文を流用して not を使うことで実現できます：

import matplotlib.pyplot as plt
import numpy as np
N = 40
xmin = -2
xmax = 2
def H0(x):
   if not x < 0: return 0  # not が加わっています
   else: return 1
p = np.linspace( xmin, xmax, N)
plt.plot( p, [H0(p[k]) for k in range(N)] )
plt.show()

f:id:pianofisica:20200928145314p:plain

if - elif - else

条件が複数ある場合には elif を使います：

$\qquad\displaystyle{ H_1(x)=\begin{cases} \ 0 & (x<-1,\ 1< x) \\ \ 1 & \text {(otherwise)} \end{cases}}$

import matplotlib.pyplot as plt
import numpy as np
N = 40
xmin = -2
xmax = 2
def H1(x):
   if x < -1: return 0
   elif x > 1: return 0  # elifが加わりました
   else: return 1
p = np.linspace( xmin, xmax, N)
plt.plot( p, [H1(p[k]) for k in range(N)] )
plt.show()

f:id:pianofisica:20200928150227p:plain

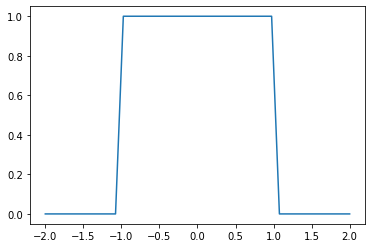
or

上の例で if - elif - else を使って定義した関数 $H_1(x)$ は、or を使っても定義できます：

import matplotlib.pyplot as plt
import numpy as np
N = 40
xmin = -2
xmax = 2
def H1a(x):
   if x < -1 or x > 1: return 0
   else: return 1
p = np.linspace( xmin, xmax, N)
plt.plot( p, [H1a(p[k]) for k in range(N)] )
plt.show()

and

複数の条件が同時にみたされている場合を扱うには and を使います：

$\qquad\displaystyle{ H_2(x)=\left\{\begin{array}{ll} \ 0 & (-1< x <1) \\ \ 1 & \text {(otherwise)}\end{array}\right.}$

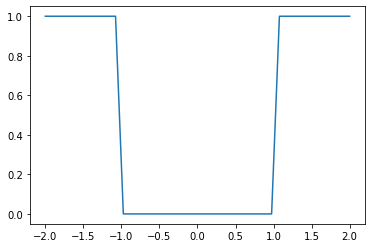
import matplotlib.pyplot as plt
import numpy as np
N = 40
xmin = -2
xmax = 2
def H2(x):
   if -1 < x and x < 1: return 0
   else: return 1
p = np.linspace( xmin, xmax, N)
plt.plot( p, [H2(p[k]) for k in range(N)] )
plt.show()

ここで -1 < x and x < 1 としている部分は、より簡潔に -1 < x < 1 とすることもできます。

f:id:pianofisica:20200928151956p:plain

キーワード：Python、条件分岐