数学の具体的な計算にPythonを使って、数学もPythonも同時に学んでしまいましょう。今回はPythonを使って、拡散方程式と呼ばれる偏微分方程式を調べたいと思います。偏微分方程式の数値的解法の導入、本記事で使っている記法の詳細については以下の記事で解説しています:
あわせて読んでみてください。
拡散方程式
上に引用した過去記事では、輸送方程式
を考え、その解析解と数値解を比較しつつ、偏微分方程式の数値計算の手法(差分法)について解説しました。本記事では、問題をもう1ステップ高度にして、拡散方程式(熱方程式、熱伝導方程式とも)と呼ばれる偏微分方程式
を考えてみます。簡単のために、ここでは は定数としましょう。本質的な違いは、右辺の1階微分が2階微分に置き換わったことです。
熱核
方程式 を境界条件
のもとで解くために、(唐突ではありますが)熱核(heat kernel) を導入します:
性質を少し調べてみましょう。まず方程式 の微分演算子を作用させてみます:
import sympy as sp x, y = sp.symbols('x, y', real = True) t, D = sp.symbols('t, D', positive = True) def K(t,x,y): return 1/sp.sqrt(4*sp.pi*D*t) * sp.exp(-(x-y)**2/(4*D*t)) Eq = sp.diff(K(t,x,y), (t, 1)) - D * sp.diff(K(t,x,y), (x, 2)) sp.simplify(Eq)
より
であって、熱核は拡散方程式の"解"であることがわかります。次に、 を固定して、
に関して実軸全体にわたって積分してみます:
sp.integrate( K(t,x,y), (y, -sp.oo, sp.oo) )
よって
です。また、 として、いくつかの
の値に対する関数の概形を図示してみます(
とします):
import matplotlib.pyplot as plt import numpy as np T = [1e0, 1e-1, 1e-2, 1e-3, 1e-4] for t in T: X = np.linspace( -5, 5, int(1e5) ) Y = 1/( 4 * np.pi * t ) * np.exp( -X**2 / (4*t) ) plt.plot(X, Y) plt.show()





グラフは左から順に です。以上から、熱核
は
を小さく取るほど
の点に局在する関数であり、
の極限でDiracのデルタ関数を与えることがわかります:
熱核を用いた解
さて、もともと考えていた問題だった、方程式 の境界条件
のもとでの解ですが、それは熱核を用いて
で与えられます。これを確かめます。まず方程式 に代入してみます:
ここで上で見た性質 を使いました。よって確かに方程式の解になっています。次に境界条件をチェックしてみます:
ここで性質 およびデルタ関数の性質を使っています。よって境界条件も満たされています。
差分方程式
差分化の手法については過去記事で扱っているので、その導入については省略します。ポイントとなるのは2階偏導関数の差分化です。2つのTaylor展開
の両辺を足し合わせると
より
です。よって2階微分の差分化として
とすることができます。以上から に対応する差分方程式として
を立式できます。ただし、時間微分に関する1階偏導関数については中心差分をとりました。式を整理すると
となります。境界条件から は既知です。しかしこの漸化式を解くためには、
の情報も必要になります。そこで、
についてのみ、時間微分について前進差分を用いることにします:
Pythonによる実装
境界条件を
として、上記の定式化をPythonで実装してみましょう。まず入力値です。
Nt = 100 Nx = 200 D = 0.5 tmin = 0.0 tmax = 3.0 xmin = -15.0 xmax = 15.0 ht = ( tmax - tmin ) / Nt hx = ( xmax - xmin ) / Nx
次に境界条件の関数の配位を表示してみます。
X = [] f0 = [] for n in range(Nx): X.append( xmin + n*hx ) f0.append(np.exp(-X[n]**2/2)) n += 1 import matplotlib.pyplot as plt plt.xlim(-2.0, 2.0) # x軸の表示範囲 plt.ylim(-.25, 1.25) # y軸の表示範囲 plt.plot( X, f0 ) plt.show()
より次のグラフを得ます。

次に を求めます:
f1 = [(f0[0]+f0[1])/2] # 差分方程式から求まらない点は前の値を引き継ぐことにしました for n in range(1,Nx-1): f1.append( D*ht/(hx**2) * (f0[n+1] - 2*f0[n] + f0[n-1]) + f0[n] ) n += 1 f1.append((f0[Nx-1]+f0[Nx-2])/2) # 差分方程式から求まらない点は前の値を引き継ぐことにしました
と合わせて図示してみます。
plt.xlim(-2.0, 2.0) plt.ylim(-.25, 1.25) plt.plot( X, f0 ) plt.plot( X, f1 ) plt.show()

逐次的に差分方程式から を求めます:
F = [f0,f1] for m in range(2,Nt-2): f = [(F[m-1][0]+F[m-1][1])/2] # 差分方程式から求まらない点は前の値を引き継ぐことにしました for n in range(1, Nx-1): f.append( 2*D*ht/(hx**2) * (F[m-1][n+1] - 2*F[m-1][n] + F[m-1][n-1]) + F[m-2][n] ) n += 1 f.append((F[m-1][Nx-1]+F[m-1][Nx-2])/2) F.append(f) m += 1
関数の時間発展のタイムラプスを作成してみます。
for k in range(5): plt.xlim(-2.0, 2.0) plt.ylim(-.25, 1.25) plt.plot( X, F[4*k] ) k += 1 plt.show()
から次のグラフを得ます:

初期状態のガウス関数(青線)から橙→緑→赤→紫と、時間の経過とともに山の高さが徐々に低くなって裾が広がっていく様子がわかります。これは温度の高い部分が、低い部分にじわじわと移っていく現象を表しています(熱伝導)。
解析解との比較
さて、解析解は で与えられました。ゆえに、境界条件
のもとでは
x, y = sp.symbols('x, y', real = True) t, D = sp.symbols('t, D', positive = True) def K(t,x,y): return 1/sp.sqrt(4*sp.pi*D*t) * sp.exp(-(x-y)**2/(4*D*t)) def phi(y): return sp.exp(-y**2/2) sol = sp.integrate( K(t,x,y) * phi(y), (y, -sp.oo, sp.oo) ) sp.simplify(sol)
より
となります。これを数値計算の重ね合わせてグラフに表示し、見比べてみます。
D = 0.5 T = [] for k in range(5): T.append( tmin + 4*ht*k ) for n in range( len(T) ): X = np.linspace( xmin, xmax, Nx ) Y = 1/np.sqrt( 2 * D * T[n] + 1 ) * np.exp( - X**2 / ( 2 * ( 2 * D * T[n] + 1 ) ) ) plt.plot(X, Y) plt.plot( X, F[4*n] ) plt.show()


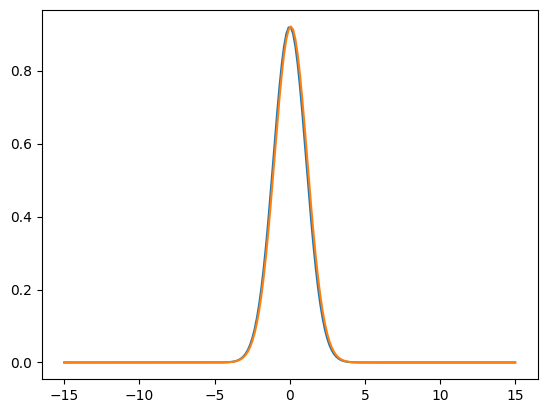


よって熱核を用いた解析解と数値的に求めた解とが一致することが確認できました。