数学・物理学の具体的な計算にPythonを使って、数学・物理学もPythonも同時に学んでしまいましょう。前回の記事
では、Pythonを使って振動を表す運動方程式(2階常微分方程式)の解を数値的に求めました。また
では、数値解によって記述される質点の運動の様子をアニメーションによって可視化してみました。
今回の記事はこれらの続編・応用で、複数の質点が互いにバネでつながれた、いわゆる連成振動について取り上げてみたいと思います。
バネにつながれた1質点の運動(単振動)
解析的解法
質量 をもつ質点の平衡点からの変位を
とします(図1上部)。質点の左右はそれぞれバネ定数
をもつバネでつながっているものとしましょう。この質点の運動方程式は以下で与えられます:

運動方程式の一般解は
で与えられます。ここで は積分定数で、初期条件によって決定されます。また
は振動の各速度を与えます。よって振動の周期は
によって与えられます。
数値的解法
運動の様子を図示するために運動方程式を数値的に解いてアニメーションを作成してみましょう。その方法の詳細については上記の過去記事の解説を参照してください。簡単のために 、
とし、初期条件として
とします。ここでは必要なコードだけ載せておきます:
N = 3000 # ステップ数 h = 0.01 # 差分間隔 T = [0] # 初期時刻 X1 = [1] # 初期位置 V1 = [0] # 初期速度 # 差分方程式 def t(k): return h+T[k-1] def x1(k): return X1[k-1]+h*(V1[k-1])+h**2/2*(-X1[k-1]) def v1(k): return V1[k-1]+h*(-X1[k-1])+h**2/2*(-V1[k-1]) for k in range(N): T.append( t(k+1) ) X1.append( x1(k+1) ) V1.append( v1(k+1) ) %matplotlib inline # JupyterNotebookでアニメーションを表示させるために必要です import matplotlib.animation as animation import matplotlib.pyplot as plt fig = plt.figure() # グラフの設定 plt.axes().set_aspect('equal') plt.xlim(-1.5, 1.5) # x軸の表示範囲 plt.ylim(-0.5, 0.5) # y軸の表示範囲 # アニメーションのフレームの作成 frames = [] num_frames = int(N/10) for i in range(num_frames): x = X1[10*i] # アニメーションのためにプロットするデータ点は10個おき y = 0 frame = plt.scatter(x, y, color='blue') frames.append([frame]) # アニメーションの描画 ani = animation.ArtistAnimation(fig, frames, interval=50) # GIFファイルとして保存 & アニメーションの表示 from IPython.display import Image f = r'harmonic_ani.gif' writergif = animation.PillowWriter(fps=50) ani.save(f,writer=writergif) plt.close() Image(open('harmonic_ani.gif','rb').read())
以上から次のようなアニメーションが出力されるとともに、ローカルに harmonic_ani.gif というファイル名のGIFファイルが作成されるはずです:
バネにつながれた2質点の運動(連成振動)
解析的解法
問題設定を拡大して、図1下部のような2つの質点がバネでつながっている場合を考えてみましょう。各質点の平衡点からの変位をそれぞれ とすると運動方程式は以下で与えられます:
よって行列を用いて
と書き表せることがわかります。右辺の行列 の各成分がすべて定数パラメタで構成されていること、そして適当な正則行列
(具体形はあとで述べます)によって行列
が対角化できることに注意します:
ここで
がいずれも正の値であることから、行列 の固有値は正定値であり、したがってそれらの正の根号がとれることを使いました。2次の単位行列を
として
であること、そして が定数行列であることから
が時間微分をすり抜けることに注意して、行列表記した運動方程式の両辺に
を掛けてみます:
となることがわかります。さらに
として新たな変数 を導入すると、運動方程式が2つの独立な単振動の式
に帰着することがわかります。その一般解は
で与えられますから、最終的に求めていた解は
となります。
一応、対角化するための正則行列 を求めておきましょう:
import sympy as sp sp.init_printing() sp.var('k1, k2, k3, m1, m2', positive=True) K = sp.Matrix([[(k1+k2)/m1, -k2/m1],[-k2/m2, (k2+k3)/m2]]) L, W = K.diagonalize() L
から、行列 の具体形が出力されます。そして対角化された行列
が
W
によって出力されます。ただいずれも、3つのバネ定数、2つの質量、とパラメタの数が多いため各成分はこれらの複雑な式になります。 となることを確認してみましょう:
sp.cancel(sp.simplify( L**(-1)*K*L - W ))
から、確認できます。単純な場合として
としてみます:
sp.cancel(L.subs(m2, m1).subs(k2,k1).subs(k3,k1))
および
sp.cancel(W.subs(m2, m1).subs(k2,k1).subs(k3,k1))
から
であることがわかります。
数値的解法
1質点の場合と同様に数値的に解いてみます。運動方程式を1階化します:
これらから展開式
を得ます。 についても同様です。ここから差分方程式が作れて、以下のコードのようにして数値計算できます:
N = 6000 # ステップ数 h = 0.01 # 差分間隔 T = [0] # 初期時刻 X1 = [-0.8] # 質点1の初期位置 V1 = [-0.3] # 質点1の初期速度 X2 = [0.1] # 質点2の初期位置 V2 = [-0.4] # 質点2の初期速度 # パラメタ値の設定 m1 = 1.0 m2 = 6.0 k1 = 1.0 k2 = 2.0 k3 = 5.0 # 差分方程式 def t(k): return h+T[k-1] def x1(k): return X1[k-1]+h*(V1[k-1])+h**2/2*( -(k1+k2)/m1*X1[k-1] + k2/m1*X2[k-1] ) def v1(k): return V1[k-1]+h*( -(k1+k2)/m1*X1[k-1] + k2/m1*X2[k-1] )\ +h**2/2*( -(k1+k2)/m1*V1[k-1] + k2/m1*V2[k-1] ) def x2(k): return X2[k-1]+h*(V2[k-1])+h**2/2*( k2/m2*X1[k-1] - (k2+k3)/m2*X2[k-1] ) def v2(k): return V2[k-1]+h*( k2/m2*X1[k-1] - (k2+k3)/m2*X2[k-1] )\ +h**2/2*( k2/m2*V1[k-1] - (k2+k3)/m2*V2[k-1] ) for k in range(N): T.append( t(k+1) ) X1.append( x1(k+1) ) V1.append( v1(k+1) ) X2.append( x2(k+1) ) V2.append( v2(k+1) ) %matplotlib inline # JupyterNotebookでアニメーションを表示させるために必要です import matplotlib.animation as animation import matplotlib.pyplot as plt fig = plt.figure() # グラフの設定 plt.axes().set_aspect('equal') plt.xlim(-3.0, 3.0) # x軸の表示範囲 plt.ylim(-0.5, 0.5) # y軸の表示範囲 # アニメーションのフレームの作成 frames = [] num_frames = int(N/15) for i in range(num_frames): y = 0 x1 = X1[15*i] -1.0 # アニメーションのためにプロットするデータ点は15個おき x2 = X2[15*i] +1.0 frame1 = plt.scatter(x1, y, color='blue') frame2 = plt.scatter(x2, y, color='orange') frames.append([frame1,frame2]) # アニメーションの描画 ani = animation.ArtistAnimation(fig, frames, interval=30) # GIFファイルとして保存 & アニメーションの表示 from IPython.display import Image f = r'two_harmonics_ani.gif' writergif = animation.PillowWriter(fps=30) ani.save(f,writer=writergif) plt.close() Image(open('two_harmonics_ani.gif','rb').read())
から以下のGIFアニメーションが作成されます:
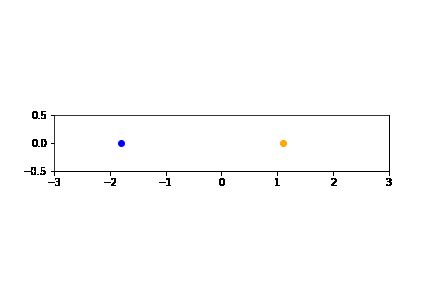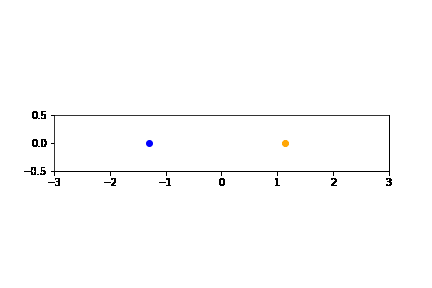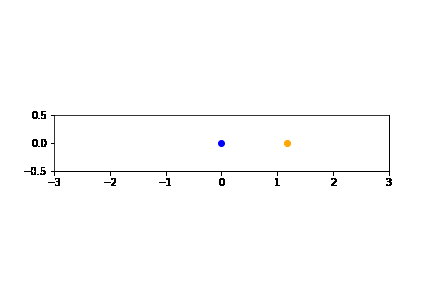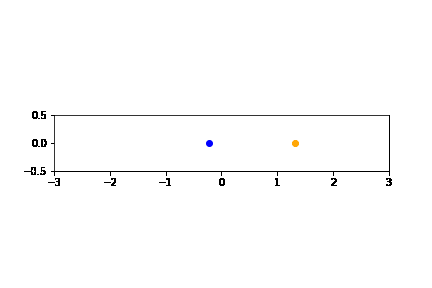
解析的な方法でみたように、適当な変換によって2つの質点の運動は2つの単振系に帰着されます。しかしながら、質点1と質点2の運動そのものを見ると、なかなか複雑な動きをしていることがわかりますね。