Pythonで描くベクトル場

数学の具体的な計算にPythonを使って、数学もPythonも同時に学んでしまいましょう。今回はPythonを使って、ベクトル場を描写したいと思います。ベクトル場を分析するにあたり、いわゆるベクトル解析の知識を少し使います。Pythonでのベクトル解析については以下の記事で扱っています：

pianofisica.hatenablog.com
pianofisica.hatenablog.com

あわせて読んでみてください。

ベクトル場の描画

ベクトル場の描画

具体例１（一様なベクトル場）

一様なベクトル場 $(V_x,V_y)=(2,1)$ は次のようにして描画できます：

import numpy as np
import matplotlib.pyplot as plt

plt.figure()

# 表示範囲の設定
Lx, Ly = 3. , 3.   

# メッシュの生成
gridWidth = float(1/2)
X, Y= np.meshgrid(\
    np.arange(-Lx, Lx, gridWidth),\
    np.arange(-Ly, Ly,gridWidth))  

# ベクトル場 (Vx, Vy)の入力
Vx = 2.
Vy = 1.

# ベクトル場の描画
plt.quiver(X,Y,Vx,Vy,color='grey')

plt.xlim([-Lx,Ly])
plt.ylim([-Ly,Ly])

# グラフの描画
plt.grid()
plt.draw()
plt.show()

より次の図を得ます：

具体例２（２次元流体力学の複素ポテンシャル）

位置に依存するベクトル場として $(V_x,\, V_y)=(x^2-y^2,\, -2xy)$ を考えてみましょう。

Vx = X**2 - Y**2
Vy = - 2*X*Y

plt.quiver(X,Y,Vx,Vy,color='grey')

plt.xlim([-Lx,Ly])
plt.ylim([-Ly,Ly])

plt.grid()
plt.draw()
plt.show()

によって、ベクトル場の様子が次のように図示されます：

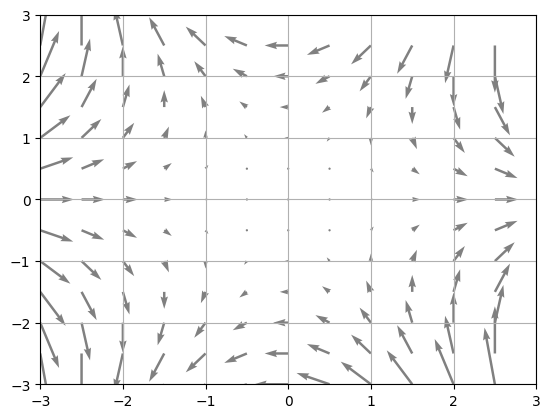
実はこのベクトル場はちょっと特殊な性質を持っています。これを示すために、ベクトル解析の計算を少しやってみます（詳しい計算については過去記事を参照してください）：

import sympy as sp
sp.var(' x y z ', real= True)

def grad(f):
    return sp.expand(sp.Matrix([[sp.diff(f,x)],[sp.diff(f,y)],[sp.diff(f,z)]]))
def div(V):
    return sp.expand(sp.diff(V[0,0],x)+sp.diff(V[1,0],y)+sp.diff(V[2,0],z))
def rot(V):
    return sp.expand(sp.Matrix(\
    [[sp.diff(V[2,0],y)-sp.diff(V[1,0],z)],\
    [sp.diff(V[0,0],z)-sp.diff(V[2,0],x)],\
    [sp.diff(V[1,0],x)-sp.diff(V[0,0],y)]]))

V = sp.Matrix([[x**2-y**2],[-2*x*y],[0]])

[div(V),rot(V)]

から

$\qquad\displaystyle{{\rm div}\,\vec{V}=0, \qquad {\rm rot}\,\vec{V}=0}\qquad(\ast)$

がわかります。まず第２の式から、ベクトル場 $\vec{V}$ が適当な関数 $f$ によって

$\qquad\displaystyle{\vec{V}={\rm grad}\,f}$

と書けることがわかります（ポアンカレの補題）。実際、 $f$ として

$\qquad\displaystyle{f=\frac{1}{3}(x^3-3xy^2)}$

ととることで、ベクトル場 $\vec{V}$ が得られます：

f = sp.Rational(1,3)*(x**3 - 3*x*y**2) 

grad(f)

さらに、この事実と、 $(\ast)$ の第１の式とから

$\qquad\displaystyle{0={\rm div}\,\vec{V}={\rm div}\,{\rm grad}\,f=\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}\right)f}$

（ここで自明な $z$ 方向の微分は落としました）であり、ここで得た関数 $f$ は２次元ラプラス方程式の解になっていることがわかります。

さて、関数 $f=\frac{1}{3}(x^3-3xy^2)$ を因数分解すると

$\qquad\displaystyle{f=\frac{1}{3}x(x-\sqrt{3}y)(x+\sqrt{3}y)}$

ですから、零点集合 $f(x,y)=0$ は次の３つの直線によって与えられることがわかります：

$\qquad\displaystyle{\ell_1:x=0,\qquad\ell_2:x-\sqrt{3}y=0,\qquad\ell_3:x+\sqrt{3}y=0}$

これらの直線とベクトル場を重ねて図示してみましょう：

Q = np.linspace( -Ly, Ly, int(1e2) )
P1 = np.zeros(int(1e2))
P2 = np.sqrt(3)*Q
P3 = -np.sqrt(3)*Q

plt.quiver(X,Y,Vx,Vy,color='grey')

plt.xlim([-Lx,Ly])
plt.ylim([-Ly,Ly])

plt.grid()
plt.draw()
plt.plot(P1, Q)
plt.plot(P2, Q)
plt.plot(P3, Q)
plt.show()

図から読み取れることは、これら３本の直線とベクトル場 $\vec{V}$ が直交していることです。実際に計算して確かめてみましょう：

def Dot(A, B):
    return sp.expand((A.transpose()*B)[0,0])

e1 = sp.Matrix([[0],[1],[0]])
e2 = sp.Matrix([[sp.sqrt(3)],[1],[0]])
e3 = sp.Matrix([[sp.sqrt(3)],[-1],[0]])

[Dot(V.subs(x, 0),e1), Dot(V.subs(x, sp.sqrt(3)*y),e2), Dot(V.subs(x, -sp.sqrt(3)*y),e3)]

さらに、次の関数

$\qquad\displaystyle{g=-\frac{1}{3}y(y-\sqrt{3}x)(y+\sqrt{3}x)}$

の零点 $g(x,y)=0$ を考えると、今度はベクトル場 $\vec{V}$ と平行する（流れが収斂する）方向になっていることがわかります：

R = np.linspace( -Lx, Lx, int(1e2) )
S1 = np.zeros(int(1e2))
S2 = np.sqrt(3)*R
S3 = -np.sqrt(3)*R

plt.quiver(X,Y,Vx,Vy,color='grey')

plt.xlim([-Lx,Ly])
plt.ylim([-Ly,Ly])

plt.grid()
plt.draw()
plt.plot(R, S1)
plt.plot(R, S2)
plt.plot(R, S3)
plt.show()

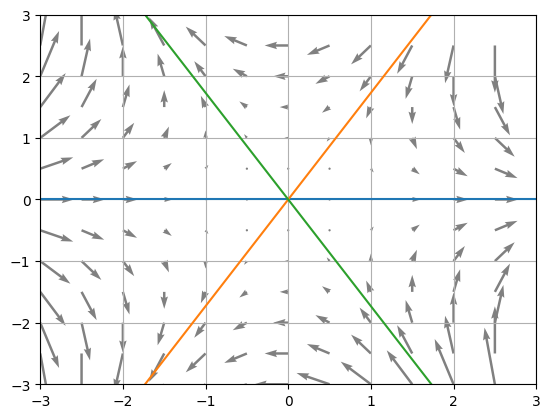
タネ明かし

何かトリックがありそうですね。唐突ですが、２次元座標 $(x,y)$ から複素数 $z$ を

$\qquad\displaystyle{z=x+iy}$

によって導入してみましょう。すると

z = x + sp.I*y
F = sp.expand(z**2)
[sp.re(F), sp.im(F)]

より

$\qquad\displaystyle{V_x={\rm Re}(z^2),\qquad V_y=-{\rm Im}(z^2)}$

であることがわかります。さらには

G = sp.expand(sp.Rational(1,3)*z**3)
[sp.re(G), sp.im(G)]

より

$\qquad\displaystyle{f=\frac{1}{3}{\rm Re}(z^3),\qquad g=\frac{1}{3}{\rm Im}(z^3)}$

だったことがわかります。そしてベクトル場を特徴づける直線（ベクトル場と直交する・平行する）が３本ずつあったのは、変換

$\qquad\displaystyle{z\quad\longrightarrow\quad \alpha z}$

を考えたときに、関数 $f,\,g$ を不変に保つ群の作用：

$\qquad\displaystyle{(\alpha z)^3=z^3 \quad \Longrightarrow\quad \alpha=1,\ e^{\frac{2\pi}{3}i}, \ e^{\frac{4\pi}{3}i}}$

これらの存在による帰結だったのです。まず、複素数による積が、複素平面における回転を記述したことを思い出しましょう。すると、上の例で見た直線 $\ell_2,\ \ell_3$ は、直線 $\ell_1$ にそれぞれ $^{\frac{2\pi}{3}i}, \ e^{\frac{4\pi}{3}i}$ を掛けて回転させて得られる直線に他なりません。実は、この例で取り上げたベクトル場の背後には、こういった構造が仕込まれていたのでした。

以上の事情は一般的なものであって、任意の自然数 $n$ について

$\qquad\displaystyle{f=\frac{1}{n}{\rm Re}(z^n),\qquad g=\frac{1}{n}{\rm Im}(z^n)}$

とすると

$\qquad\displaystyle{{\rm grad}\,f=\left(\frac{\partial f}{\partial x},\, \frac{\partial f}{\partial y}\right)=({\rm Re}(z^{n-1}),\, -{\rm Im}(z^{n-1}) )=\left(\frac{\partial g}{\partial y},\, -\frac{\partial g}{\partial x}\right)}$