Pythonで学ぶ確率・統計（何回転で大当たりが出る？）

数学の具体的な問題にPythonを使って、数学もPythonも同時に学んでしまいましょう。今回はPythonを使った確率・統計の問題として、くじを引き続けて何回目に当たりが出るのか考えてみたいと思います。ただし、引いたハズレくじについては毎回戻すものとし、当たりくじを引く確率は毎回一定であるものとします。これはパチンコ遊技などの大当たりを引く確率と、回転数（試行回数）との関係にも当てはまります。

くじ引きの実装
当たるまでの回数（数値的実験）
当たるまでの回数（数学的考察）
- 確率分布
- 当たるまでの回数の期待値
回転数と当たりを引く確率
余談：ネイピア数との関係

くじ引きの実装

Pythonでランダムに1から10の数字を出力させて、数字の10が出たら当たり、それ以外の数字をはずれとして、当たりの確率が1/10のくじを実現してみましょう。まず、ランダムな整数の出力は以下のようにします。

import random as rd
rd.randint(1, 10)  # randint(a,b) で a 以上 b 以下の整数をランダムに出力

それぞれの数字が出る確率は1/10のはずですから、例えば試行を10,000回繰り返してみると各数字は1,000回くらいずつ出ることが期待されます。これをヒストグラムを作成して確認してみます。

num_trial = int(1.0e4)
result = []
for k in range(num_trial):
    result.append(rd.randint(1, 10))

import matplotlib.pyplot as plt
plt.hist(result, bins=10, range=(1, 11))
plt.show()

より

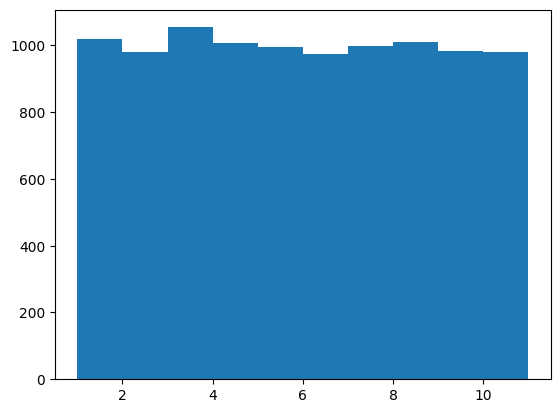
といったヒストグラム（横軸は出目、縦軸は出現回数）を得て、うまくいっていることがわかります。

ちなみに、本記事は、以下の過去記事の発展的な内容になっています。あわせて読んでいただければさいわいです。

pianofisica.hatenablog.com

当たるまでの回数（数値的実験）

さて、当たりが出るまでくじを引き続けたとき、何回目で当たりが出るでしょうか？当たりくじが出るまでくじを引き続けるというのは、while文でループさせ、if文によってbreakさせることによって実現できます。そしてループごとにカウント数を増やして、breakの前にカウント数を出力させます：

count = 1
while True:
    lot = rd.randint(1, 10)
    if lot == 10:
        print(count)
        break
    else:
        count += 1

これもランダム性から、入力するたびに出力の値が変わります。

ここで求めた、当たりが出るまでくじを引いた回数を関数として定義します。

def times_draw():
    count = 1
    while True:
        lot = rd.randint(1, 10)
        if lot == 10:
            return count
            break
        else:
            count += 1

関数の出力をリストに格納していきます。ここでは当たりが出るまでの試行を1,000回繰り返したとします。

number_trial = int(1.0e3)
time_draw_list = []
for k in range(number_trial):
     time_draw_list.append(times_draw())

ヒストグラムを出力します。

plt.hist(time_draw_list, bins=20)
plt.show()

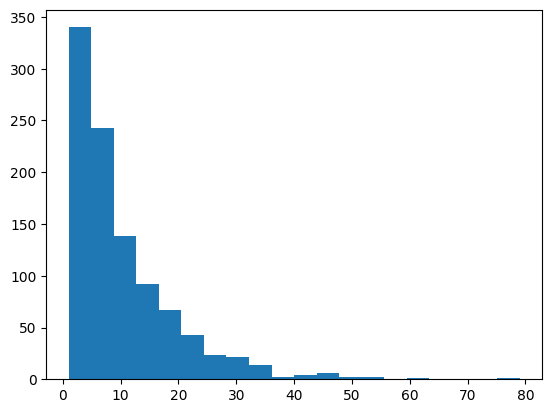
横軸は当たるまでの回数、縦軸は出現回数です。分布に指数関数的な特徴が見受けられます。

当たるまでの回数（数学的考察）

確率分布

少し数学的に問題を考察してみます。１回目に当たる確率は、設定の通り 1/10 です。では２回目に当たる確率は？といえば、やはり 1/10 なのですが、すでに２回目を引いているということは、１回目に 9/10 のはずれを引いていた、ということで、1/10 * 9/10 がその確率となります。同様にして３回目に当たる確率は 1/10 * 9/10 * 9/10 です。一般に n 回目に当たる確率を $P_n$ とすれば

$\qquad\displaystyle{P_n=\frac{1}{10}\times\left(\frac{9}{10}\right)^{n-1}}$

がわかります。問題を一般化して、当たりの確率を $p$ とすれば

$\qquad\displaystyle{P^{\rm GD}_n=p\left(1-p\right)^{n-1}}$

となります。このような確率分布を幾何分布（Geometric Distribution）といいます。また、確率論や統計学の教科書的には、１回１回のくじ引きのことは「ベルヌーイ試行（Bernoulli trial）」と呼びます。

問題の設定から、当たるまで何回でもくじを引き続けることができるので、何十回、何百回、何千回とくじを引き続ければ、いつかは必ず当たるはずです。これは数式としては

$\qquad\displaystyle{S=\sum_{n=1}^\infty P_n=1}$

を意味します。少し計算して確かめてみましょう。一般化した式で見てみます。

$\qquad\displaystyle{\begin{aligned}S&=\sum_{n=1}^\infty p(1-p)^{n-1}\\&=p\sum_{n=0}^\infty (1-p)^{n}\\&=p\left\{1+(1-p)+(1-p)^2+(1-p)^3+\dots\right\}\end{aligned}}$

ここで無限個の項の和

$\qquad\displaystyle{s=1+(1-p)+(1-p)^2+(1-p)^3+\dots}$

ですが、これは高校数学の等比級数の問題でおなじみですね：

$\qquad\displaystyle{\begin{aligned}s&=1+(1-p)+(1-p)^2+(1-p)^3+\dots\\ (1-p)s&=\quad\ \, \, (1-p)+(1-p)^2+(1-p)^3+\dots\end{aligned}}$

両辺を引き算すれば

$\qquad\displaystyle{s=\frac{1}{p}}$

がわかって、 $S=1$ が示されました。
　

当たるまでの回数の期待値

さて、問題の、当たるまで何回くじを引くのか？ですが、確率分布が求まったので、回数の重みをつけて期待値を計算します：

$\qquad\displaystyle{\mu=\sum_{n=1}^\infty n\,P_n}$

これを求めてみます。一般化した場合で考えましょう。

$\qquad\displaystyle{\begin{aligned}\mu&=p\sum_{n=1}^\infty n(1-p)^{n-1}\\&=p\sum_{n=1}^\infty \left\{-\frac{d}{dp}(1-p)^{n}\right\}\\&=-p\frac{d}{dp}\sum_{n=1}^\infty (1-p)^{n}\end{aligned}}$

ここで無限項の和は上で求めた結果を使うと

$\qquad\displaystyle{\sum_{n=1}^\infty (1-p)^{n}=(1-p)\sum_{n=0}^\infty (1-p)^{n}=\frac{1-p}{p}}$

がわかります。したがって

$\qquad\displaystyle{\mu=-p\frac{d}{dp}\left(\frac{1-p}{p}\right)}$

となります。SymPyで微分を計算すると

import sympy as sp
p = sp.var('p')
sp.simplify( -p * sp.diff( (1-p)/p , p, 1 ) )

から

$\qquad\displaystyle{\mu=\frac{1}{p}}$

がわかります。すなわち $p=1/10$ とした場合、当たりは平均10回で引き当てられることがわかります。

それでは、10回以内に当たる確率はいくらか？といえば

$\qquad\displaystyle{S_{10}=\sum_{k=1}^{10} P_k=p\sum_{k=0}^{9} (1-p)^k}$

で与えられます。等比級数の和は、有限項の場合も無限項の場合と同様ですね：

$\qquad\displaystyle{\begin{aligned}s_{10}&=1+(1-p)+(1-p)^2+\dots+(1-p)^9\\ (1-p)s_{10}&=\quad \, \, \,(1-p)+(1-p)^2+\dots+(1-p)^9+(1-p)^{10}\end{aligned}}$

より

$\qquad\displaystyle{s_{10}=\frac{1-(1-p)^{10}}{p}}$

すなわち

$\qquad\displaystyle{S_{10}=1-(1-p)^{10}=1-\left(\frac{9}{10}\right)^{10}\simeq 0.65132\dots}$

となります。よって、10回くじを引けば約65％の確率で当たりが出ることがわかります。

回転数と当たりを引く確率

上の計算から、n 回目までに当たりを引く確率が

$\qquad\displaystyle{S_{n}=\sum_{k=1}^{n} P_k=p\sum_{k=0}^{n} (1-p)^k=1-(1-p)^n}$

で与えられることがわかります。もちろん、n を無限大にすれば $S_\infty=1$ となって100％当たりが出るわけですが、現実では、くじを引くことは有限回数しかできません。回数と確率がどのような関係になっているのか調べてみましょう。

確率 1/10 の場合

p = 1/10
import matplotlib.pyplot as plt
import numpy as np
n = np.linspace( 1, 100, 200)
S = 1 - (1-p)**n
plt.plot(n, S)
plt.show()

横軸は試行回数、縦軸は、その回数までに当たりが出る確率です。いくつか代表的な値を拾ってみましょう：

def S(n):
    p = 1/10
    return (1 - (1-p)**n) * 100
[S(1), S(2), S(5), S(10), S(20), S(30)]

表にまとめると以下のようになります：

回数	1	2	5	10	20	30
確率	10.0％	19.0％	41.0％	65.1％	87.8%	95.7%

当たりの確率が10％のくじを、10回引いたところで約35％、20回引いたとしても10％以上の確率で当たりは出ないことがわかります。また、当たりが出る確率が99％を超えるのは、n=44 のときです。

Youtubeなどの動画投稿サイトでは、トレーディングカードのパック開封や、スクラッチくじ、パチンコ・スロットマシーンなどを多くの人たちがやっている様子を見ることができますが、なかなか狙い通りに当たっていないことも、数字で見ると納得できると思います。

以下、当たりの確率を変えて同様の分布を求めてみます。

確率 1/50 の場合

回数	50	100	150	200
確率	63.6％	86.7％	95.2％	98.2%

確率 1/100 の場合

回数	100	200	300	400
確率	63.4％	86.6％	95.1％	98.2%

確率 1/320 の場合

回数	320	640	960	1280
確率	63.3％	86.5％	95.0％	98.2%

余談：ネイピア数との関係

さて、いくつかの例で $p=1/N$ として $S_N,\ S_{2N},\ S_{3N},\ S_{4N}$ を求めてみました。よく見ると、異なる $N$ の値を設定していたにもかかわらず、これらはいずれもほぼ同一の値を与えています。なぜでしょうか？式を見ると

$\qquad\displaystyle{S_{N}=1-\left(1-\frac{1}{N}\right)^N}$

です。これを $N$ の関数とみなしてグラフに描いてみます。

N = np.linspace( 2, 300, 200)
Sn = 1 - (1-1/N)**N
plt.plot(N, Sn)
plt.show()

より

となります。よってNの小さい領域では値は大きく変化しますが、Nがじゅうぶん大きな領域では、変化がゆるやかになり明らかに一定の値に収束しています。答えをいえば

$\qquad\displaystyle{\lim_{N\to\infty}S_{N}=1-\lim_{N\to\infty}\left(1-\frac{1}{N}\right)^N=1-\frac{1}{e}\simeq0.63212\dots}$

となります。ここで $e$ はネイピアの数、自然対数の底です。同様に

$\qquad\displaystyle{\begin{aligned}\lim_{N\to\infty}S_{2N}&=1-\lim_{N\to\infty}\left(1-\frac{1}{N}\right)^{2N}=1-\frac{1}{e^2}\simeq0.86466\dots\\ \lim_{N\to\infty}S_{3N}&=1-\lim_{N\to\infty}\left(1-\frac{1}{N}\right)^{3N}=1-\frac{1}{e^3}\simeq0.95021\dots\\ \lim_{N\to\infty}S_{4N}&=1-\lim_{N\to\infty}\left(1-\frac{1}{N}\right)^{4N}=1-\frac{1}{e^4}\simeq0.98168\dots\end{aligned}}$

などとなります。こんな考察からも数学定数のネイピア数が出てくることがわかって、数学の不思議さ・面白さが感じられますね。

キーワード：Python、確率・統計、乱数、ヒストグラム