Python（SymPy）で学ぶシュレーディンガー方程式（１次元調和振動子）

物理学の具体的な計算にPython（SymPy）を使って、物理学もPython（SymPy）も同時に学んでしまいましょう。今回はPython（SymPy）を使ってシュレーディンガー方程式を解いてみたいと思います。シュレーディンガー方程式は量子力学の基礎方程式です。この記事で取り上げるのは１次元調和振動子の問題です。

Python（SymPy）のごく基本的な使い方については以下の記事を参照してください：

pianofisica.hatenablog.com

正準交換関係
１次元調和振動子のハミルトニアン
生成・消滅演算子
エネルギー固有値
基底状態の波動関数の具体形
励起状態の波動関数の具体形
エルミート多項式
波動関数の図示

正準交換関係

まず前提として、量子力学では古典的な物理量にはエルミート演算子が対応します。とくに質点の位置座標と運動量に対応する演算子、位置演算子 $\hat{x}$ と運動量演算子 $\hat{p}$ は次の正準交換関係をみたします。

$\quad\displaystyle{ [\hat{x},\hat{p}]=i\hbar}$

ここに角括弧は交換子で、２つの演算子 $\hat{A}$ と $\hat{B}$ に対して

$\quad\displaystyle{ [\hat{A},\hat{B}]=\hat{A}\hat{B}-\hat{B}\hat{A}}$

と定義します。

１次元空間の波動関数 $\psi(x)$ に対しては位置演算子 $\hat{x}$ と運動量演算子 $\hat{p}$ は

$\quad\displaystyle{ \hat{x}\psi(x)=x\psi(x)\qquad\hat{p}\psi(x)=-i\hbar\frac{d}{dx}\psi(x)}$

と作用するものと定義します。

実際、このように演算子の作用を定義すると、 $x$ の任意のなめらかな関数 $f(x)$ に対して

$\quad\displaystyle{\begin{aligned} {[ \hat{x},\hat{p} ]}\, f(x)&=\left(\hat{x}\hat{p}-\hat{p}\hat{x}\right)f(x)\\ &=-i\hbar\left(x\frac{d}{dx}-\frac{d}{dx}\,x \right)f(x)\\ &=+i\hbar\, f(x)\end{aligned}}$

となり、 $x$ の関数の空間の上で確かに交換関係が成り立っていることがわかります。

この計算自体は難しいものではないですが、これはPython（SymPy）では以下のようにして計算できます。

%reset -f
import sympy as sp

sp.var('h', positive = True)  # プランク定数
sp.var('x')

from sympy.core.function import Function

f = Function('f')(x)    #  座標 x に依存する任意関数

def X(f): return x*f   #  位置演算子 x の関数への作用
def P(f): return -sp.I*h*sp.diff(f,x)   #  運動量演算子 p の関数への作用

sp.expand(X(P(f))-P(X(f)))   #  交換子

１次元調和振動子のハミルトニアン

１次元調和振動子の（古典力学的）ハミルトニアンは

$\quad\displaystyle{ {H}=\frac{{p}^2}{2m}+\frac{k{x}^2}{2} }$

で与えられます。ここで $m$ は質点の質量、 $k$ はバネ定数です。いま

$\quad\displaystyle{ \omega=\sqrt{\frac{k}{m}} \qquad\quad k=m\omega^2 }$

とすればハミルトニアンは

$\quad\displaystyle{ {H}=\frac{{p}^2}{2m}+\frac{m\omega^2{x}^2}{2} }$

と書き直されます。ハミルトン形式による古典的な運動の定式化では、物理量 $O$ に対する時間発展は

$\quad\displaystyle{ \frac{d O}{dt}=\{ O, H \} }$

で与えられます。ここで波括弧はポアソン括弧で

$\quad\displaystyle{ \{ A, B \}=\frac{\partial A}{\partial x}\frac{\partial B}{\partial p}-\frac{\partial A}{\partial p}\frac{\partial B}{\partial x} }$

によって定義されます。

したがって、とくに質点の位置座標 $x$ と運動量 $p$ の時間発展は

$\quad\displaystyle{\begin{aligned} \frac{d x}{dt}&=\{ x, H \}=\frac{\partial H}{\partial p}=\frac{p}{m}\\ \frac{d p}{dt}&=\{ p, H \}=-\frac{\partial H}{\partial x}=-kx \end{aligned}}$

ですが、２つの式から運動量 $p$ を消去すれば

$\quad\displaystyle{ m\frac{d^2 x}{dt^2}=-kx }$

というお馴染みの１次元調和振動子の運動方程式が得られます。

さて、ハミルトニアンが物理量の二乗の和になっていることから、因数分解して

$\quad\displaystyle{\begin{aligned} {H}&=\hbar \omega\left(\frac{{p}^2}{2\hbar m \omega}+\frac{m\omega}{2\hbar}{x}^2 \right)\\ &=\hbar \omega \left(\sqrt{\frac{m\omega}{2\hbar}} x-\frac{ip}{\sqrt{2\hbar m \omega}}\right) \left(\sqrt{\frac{m\omega}{2\hbar}} x +\frac{ip}{\sqrt{2\hbar m \omega}}\right) \end{aligned} }$

と書き表してみましょう。

生成・消滅演算子

ハミルトニアンを上のように因数分解した形から、生成・消滅演算子をそれぞれ

$\quad\displaystyle{ \hat{a}^\dagger=\sqrt{\frac{m\omega}{2\hbar}} \hat{x}-\frac{i\hat{p}}{\sqrt{2\hbar m \omega}} \qquad\qquad \hat{a}=\sqrt{\frac{m\omega}{2\hbar}} \hat{x} +\frac{i\hat{p}}{\sqrt{2\hbar m \omega}} }$

と定義してみます。するとこれらの交換関係が

$\quad\displaystyle{ [\hat{a},\hat{a}^\dagger]=1 }$

と計算されます。実際、Pythonで計算すると

sp.var('m, w', positive = True)

def a(f): return sp.sqrt(m*w/(2*h))*X(f)+sp.I/sp.sqrt(2*h*m*w)*P(f)
def ad(f): return sp.sqrt(m*w/(2*h))*X(f)-sp.I/sp.sqrt(2*h*m*w)*P(f)

sp.cancel(a(ad(f))-ad(a(f)))

より、確かに上の交換関係が成り立っています。

エネルギー固有値

いまハミルトニアンは演算子になっているので、各項の積の順序に注意しながら書き直すと

$\quad\displaystyle{ \begin{aligned} \hat{H} &=\frac{\hat{p}^2}{2m}+\frac{m\omega^2\hat{x}^2}{2} \\ &=\hbar \omega \left (\sqrt{\frac{m\omega}{2\hbar}} \hat{x}-\frac{i\hat{p}}{\sqrt{2\hbar m \omega}} \right) \left( \sqrt{\frac{m\omega}{2\hbar}} \hat{x} +\frac{i\hat{p}}{\sqrt{2\hbar m \omega}} \right) - \frac{i\omega}{2}[\hat{x},\hat{p}] \\ &=\hbar\omega\left(\hat{a}^\dagger\hat{a}+\frac{1}{2}\right) \end{aligned} }$

がわかります。

いま基底状態の波動関数 $\psi_0(x)$ を、消滅演算子を使って

$\quad\displaystyle{ \hat{a}\psi_0(x)=0 }$

となる非自明な関数として決めます。

すると、この波動関数 $\psi_0(x)$ はハミルトニアンの固有状態で

$\quad\displaystyle{ \hat{H}\psi_0(x)=\frac{\hbar\omega}{2}\psi_0(x) }$

より、その固有値は $\hbar\omega/2$ であることがわかります。

またこの波動関数 $\psi_0(x)$ から、ハミルトニアンの固有状態が以下のようにして構成できます：

$\quad\displaystyle{ \psi_n(x)=C_n \left(a^\dagger\right)^n\psi_0(x) }$

ここで $C_n$ は規格化のための定数で、規格化条件

$\quad\displaystyle{ 1=\int_{-\infty}^\infty dx\, \left| \psi_n\right|^2 }$

によって決めます。このように構成した関数 $\psi_n(x)$ に対してハミルトニアンを作用させると

$\quad\displaystyle{\begin{aligned} \hat{H}\psi_n&=C_n \hbar\omega\left(\hat{a}^\dagger\hat{a}+\frac{1}{2}\right)\left(a^\dagger\right)^n\psi_0 \\ &=C_n \hbar\omega\left(\hat{a}^\dagger\hat{a}\left(a^\dagger\right)^n+\frac{\left(a^\dagger\right)^n}{2}\right)\psi_0 \\ &=C_n \hbar\omega\left(\hat{a}^\dagger\left[\hat{a},\left(a^\dagger\right)^n\right]+\left(a^\dagger\right)^{n+1}\hat{a}+\frac{\left(a^\dagger\right)^n}{2}\right)\psi_0 \\ &=C_n \hbar\omega\left(\hat{a}^\dagger\left[\hat{a},\left(a^\dagger\right)^n\right]+\frac{\left(a^\dagger\right)^n}{2}\right)\psi_0 \end{aligned}}$

となります。最後の等式では $\psi_0(x)$ の性質を使いました。

さて、交換子 $\left[\hat{a},\left(a^\dagger\right)^n\right]$ ですが、これは

$\quad\displaystyle{ \left[\hat{a},\left(a^\dagger\right)^n\right]=n\left(a^\dagger\right)^{n-1} }$

と計算されます。 $n=1$ の場合はすでに計算しました。

ある自然数 $n$ まで上記の公式が成り立っていると仮定します。

ここで公式

$\quad\displaystyle{\left[\hat{A},\hat{B}\hat{C}\right]=\hat{A}\hat{B}\hat{C}-\hat{B}\hat{C}\hat{A}= [\hat{A},\hat{B}]\hat{C}+\hat{B} [\hat{A},\hat{C}] }$

を使うと $n+1$ の場合に対して

$\quad\displaystyle{\begin{aligned} \left[\hat{a},\left(a^\dagger\right)^{n+1}\right] &= \left[\hat{a},a^\dagger\left(a^\dagger\right)^{n}\right]\\ &= \left[\hat{a},a^\dagger\right]\left(a^\dagger\right)^{n}+a^\dagger\left[\hat{a},\left(a^\dagger\right)^{n}\right]\\ &=\left(a^\dagger\right)^{n}+n\left(a^\dagger\right)^{n}\\ &=(n+1)\left(a^\dagger\right)^{n} \end{aligned}}$

となり、公式の成立が示されます。

ハミルトニアンの $\psi_n(x)$ への作用に話を戻すと

$\quad\displaystyle{\begin{aligned} \hat{H}\psi_n&=C_n \hbar\omega\left(\hat{a}^\dagger\left[\hat{a},\left(a^\dagger\right)^n\right]+\frac{\left(a^\dagger\right)^n}{2}\right)\psi_0 \\ &=C_n \hbar\omega\left(n\left(a^\dagger\right)^n+\frac{\left(a^\dagger\right)^n}{2}\right)\psi_0 \\ &= \hbar\omega \left(n+\frac{1}{2}\right)\psi_n \end{aligned}}$

となって、 $\psi_n(x)$ がハミルトニアンの固有状態で、

その固有値が $\hbar\omega \left(n+1/2\right)$ であることがわかります。

基底状態の波動関数の具体形

記号を簡単化するために、以下のようにして変数を無次元化します。

$\quad\displaystyle{\xi=\sqrt{\frac{m\omega}{\hbar}} x }$

すると消滅演算子は

$\quad\displaystyle{\hat{a}=\frac{1}{\sqrt{2}}\left(\xi+\frac{d}{d\xi}\right) }$

と表されます。したがって基底状態の波動関数 $\psi_0(x)$ に対する方程式は

$\quad\displaystyle{\left(\xi+\frac{d}{d\xi}\right)\psi_0(\xi)=0 }$

となります。これは１階線形微分方程式なので簡単に解がわかります：

$\quad\displaystyle{\psi_0(\xi)=C_0\,e^{-\frac{\xi^2}{2}} }$

もとの変数 $x$ で書き表すと

$\quad\displaystyle{\psi_0(\xi)=C_0\,e^{-\frac{m\omega x^2}{2\hbar}} }$

です。規格化条件から、位相因子 $e^{i\theta}$ の不定性を除いて

$\quad\displaystyle{C_0=e^{i\theta}\left(\frac{m\omega}{\pi\hbar}\right)^{1/4} }$

と決まります。実際

sp.var('theta', real = True)

psi0 = sp.exp(sp.I*theta)*((m*w)/(sp.pi*h))**(1/4)*sp.exp(-m*w*x**2/(2*h))

sp.integrate(psi0*sp.conjugate(psi0), (x, -sp.oo, sp.oo) )

より、たしかに規格化されていることがわかります。

励起状態の波動関数の具体形

基底状態に次々と生成演算子を作用させて励起状態が得られるので、いくつか具体的に見てみましょう。以下、物理的でない規格化の位相因子は１とします。

del(psi0)
psi0 = ((m*w)/(sp.pi*h))**(sp.Rational(1/4))*sp.exp(-m*w*x**2/(2*h))
psi0

sp.var('C1', positive = True)
psi1 = C1*ad(psi0)
c1 = sp.solve(sp.integrate(psi1*sp.conjugate(psi1), (x, -sp.oo, sp.oo))-1, C1)
psi1 = psi1.subs(C1, c1[0])
psi1

sp.var('C2', positive = True)
psi2 = C2*ad(psi1)
c2 = sp.solve(sp.integrate(psi2*sp.conjugate(psi2), (x, -sp.oo, sp.oo))-1, C2)
psi2 = sp.simplify(psi2.subs(C2, c2[0]))
psi2

sp.var('C3', positive = True)
psi3 = C3*ad(psi2)
c3 = sp.solve(sp.integrate(psi3*sp.conjugate(psi3), (x, -sp.oo, sp.oo))-1, C3)
psi3 = sp.simplify(psi3.subs(C3, c3[0]))
psi3

より

$\quad\displaystyle{\begin{aligned} \psi_1(x)&={{\sqrt{2}\,m^{{{3}\over{4}}}\,\omega^{{{3}\over{4}}}\,x\,e^ {- {{m\,\omega\, x^2}\over{2\,\hbar}} }}\over{\pi^{{{1}\over{4}}}\,\hbar^{{{3}\over{4}}}}}\\ \psi_2(x)&={{m^{{{1}\over{4}}}\,\omega^{{{1}\over{4}}}\,\left(\sqrt{2}\,m\,\omega\,x^2- {{\hbar}\over{\sqrt{2}}}\right)\,e^ {- {{m\,\omega\,x^2}\over{2\,\hbar}} }}\over{ \pi^{{{1}\over{4}}}\,\hbar^{{{5}\over{4}}}}}\\ \psi_3(x)&={{m^{{{3}\over{4}}}\,\omega^{{{3}\over{4}}}\,\left({{2\,m\,\omega\,x^3}\over{ \sqrt{3}}}-\sqrt{3}\,\hbar\,x\right)\,e^ {- {{m\,\omega\,x^2}\over{2\,\hbar}} } }\over{\pi^{{{1}\over{4}}}\,\hbar^{{{7}\over{4}}}}} \end{aligned}}$

などと求まります。あるいは無次元の変数 $\xi$ を使えば

$\quad\displaystyle{\begin{aligned} \psi_1(\xi)&=C_0 \sqrt{2}\,\xi\,e^{-\frac{\xi^2}{2}} \\ \psi_2(\xi)&=C_0\frac{(2\xi^2-1)\,e^{-\frac{\xi^2}{2}}}{\sqrt{2}}\\ \psi_3(\xi)&=C_0\frac{(2\xi^3-3\xi)\,e^{-\frac{\xi^2}{2}}}{\sqrt{3}} \end{aligned}}$

と書き表せます。ここで特徴的な多項式が現れることに注意します。

じつは、１次元調和振動子のエネルギー固有関数は、以下で説明するエルミート多項式（Hermite polynoimal） $H_n$ を使って

$\quad\displaystyle{\psi_n(\xi)=C_0\frac{H_n(\xi)\, e^{-\xi^2/2}}{2^{n/2}\sqrt{n!}} }$

と表すことができます。

エルミート多項式

エルミート多項式 $H_n(x)$ は、Rodriguesの公式によって

$\quad\displaystyle{H_n(x)=(-1)^ne^{x^2}\frac{d^n}{dx^n}e^{-x^2} }$

として求まる多項式です。具体的にいくつかあげると、

SymPyの組み込み関数からエルミート多項式を呼び出して

sp.init_printing()
x=sp.var('x')
sp.hermite(0,x)

sp.hermite(1,x)

sp.hermite(2,x)

sp.hermite(3,x)

あるいは、具体的にRodoriguesの公式を使って

def H(n): return sp.expand((-1)**n*sp.exp(x**2)*sp.diff(sp.exp(-x**2), x, n))
H(0)

H(1)

H(2)

H(3)

より（もちろん、どちらも同じ多項式を与えますが）

$\quad\displaystyle{\begin{aligned} H_0(x)&=1\\ H_1(x)&=2x\\ H_2(x)&=4x^2-2\\ H_3(x)&=8x^3-12x\\ \end{aligned}}$

といった多項式です。エルミート多項式には次の公式があります：

$\quad\displaystyle{\frac{dH_n(x)}{dx}=-H_{n+1}(x)+2xH_{n}(x) }$

この公式はRodriguesの公式を微分することで容易に示すことができます。

公式を使うと（規格化した変数で表した）生成演算子の作用のもとで

$\quad\displaystyle{\sqrt{2}\hat{a}^\dagger H_n(\xi)\, e^{-\xi^2/2}=\left(\xi-\frac{d}{d\xi}\right)H_n(\xi)\, e^{-\xi^2/2}=H_{n+1}(\xi)\, e^{-\xi^2/2} }$

が成り立つことがわかります。これにより、規格化定数を除いて $\psi_n(\xi)$ が求まります。

また、規格化定数もエルミート多項式の性質

$\quad\displaystyle{\int_{-\infty}^\infty dx \, H_m(x)H_n(x) \,e^{-x^2}=2^mm!\sqrt{\pi}\,\delta_{mn} }$

から決めることができます。この性質は具体的に

def D(m,n): return sp.integrate(H(m)*H(n)*sp.exp(-x**2), ( x,-sp.oo, sp.oo) )
sp.Matrix([
[D(0,0),D(0,1),D(0,2),D(0,3)],
[D(1,0),D(1,1),D(1,2),D(1,3)],
[D(2,0),D(2,1),D(2,2),D(2,3)],
[D(3,0),D(3,1),D(3,2),D(3,3)]])

によって確かめることができます。

波動関数の図示

エネルギー固有状関数をいくつか図示してみましょう：

Psi0 = psi0.subs(h,1).subs(m,1).subs(w,1)
Psi1 = psi1.subs(h,1).subs(m,1).subs(w,1)
Psi2 = psi2.subs(h,1).subs(m,1).subs(w,1)
Psi3 = psi3.subs(h,1).subs(m,1).subs(w,1)
sp.plot(Psi0, Psi1, Psi2, Psi3,(x, -5, 5))

として出力されたのが次の図です：

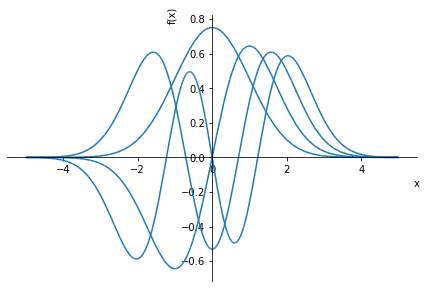
ただし、 $m$ 、 $\omega$ 、 $\hbar$ はいずれも１としています（見づらかったら、それぞれの励起状態を個別に図示してみてください）。励起状態のエネルギー固有値が上がるごとに節（ゼロ点）の個数が増えていく様子がわかります。

また、粒子の存在確率分布（波動関数の絶対値２乗） $\rho(x)=\left|\psi(x)\right|^2$ も図示してみると

sp.plot(Psi0**2, Psi1**2, Psi2**2, Psi3**2,(x, -5, 5))

により

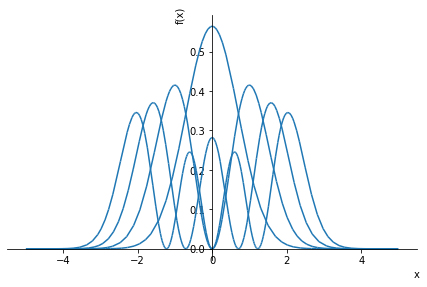
と図示されます。

さいごに粒子の存在確率分布から、粒子が存在する位置の期待値と分散を求めてみます：まず期待値

sp.integrate( x*Psi0**2, (x, -sp.oo, sp.oo))

sp.integrate( x*Psi1**2, (x, -sp.oo, sp.oo))

sp.integrate( x*Psi2**2, (x, -sp.oo, sp.oo))

sp.integrate( x*Psi3**2, (x, -sp.oo, sp.oo))

次に分散

sp.integrate( x**2*Psi0**2, (x, -sp.oo, sp.oo))

sp.integrate( x**2*Psi1**2, (x, -sp.oo, sp.oo))

sp.integrate( x**2*Psi2**2, (x, -sp.oo, sp.oo))

sp.integrate( x**2*Psi3**2, (x, -sp.oo, sp.oo))

より、いずれの状態に対しても、粒子が存在する位置の期待値 $\langle x \rangle$ はゼロとなります。このことは、波動関数の分布が原点に対して左右均等であることからもわかります。しかし、分散はエネルギー固有値が大きくなるにつれて大きくなることがわかります。このことは、波動関数の分布が高いエネルギーの状態になるにつれて、原点からより離れた点にも分布のヤマをもつことからわかります。以上、これらの計算結果は、図示した確率分布の様子と直感的にも整合します。

キーワード：Python、シュレーディンガー方程式、調和振動子、エルミート多項式、量子力学