数学の具体的な計算にMaximaを使って、数学もMaximaも同時に学んでしまいましょう。
今回はMaximaを使って円錐曲線(二次曲線)を学びたいと思います。
とくにパラメタの変化に応じた曲線の変化の様子を視覚的にわかりやすくしてみました。
画像ファイルとして出力したグラフの作成にはMaxima(とgnuplot)を、
Maximaで作成した複数のepsファイルからGIFアニメを作成するにはImageMagickを使いました。
円錐曲線(二次曲線)
円錐曲線という名前は、円錐を平面で切断したときの断面に現れる曲線であることに由来します。
数学的には、-平面上の曲線であって、変数
について2次の方程式
によって定まります。
2次の方程式によって定まる曲線ですので、円錐曲線はまた二次曲線とも呼ばれます。
以下、左辺の2次式を と呼ぶことにします。
この一般式は座標を適当に線形変換することで以下の3種類に変形・分類できます:
楕円(ellipse)
円は楕円の特別な場合( )です。
放物線(parabola)
双曲線(hyperbola)
以上の3つの形の式を円錐曲線の標準形と呼びます。
(ここでは退化した場合は考えないことにします)
次に、上で与えた一般形の2次式がどのようにして標準形に変形されるかをみていきます。
行列表示
行列を用いた2次式の記述
2次式
は行列を用いて
と表せます。このことはMaximaによって
kill(all)$ v:matrix([x],[y])$ M(a,b,c):=matrix([a,b],[b,c])$ DE:matrix([d,e])$ expand(transpose(v).M(a,b,c).v+2*transpose(DE).v+f);
から確かめられます。ここで行列
は実対称行列なので適当な線形変換によって対角化することができます。
実際、Maximaで
M(a,b,c):=matrix([a,b],[b,c])$ eigenvectors(M(a,b,c));
とすることにより、ベクトル
がそれぞれ固有値
の固有ベクトルであることがわかります。また行列
を導入すると
L:matrix([1,(c-a+sqrt((c-a)^2+4*b^2))/(2*b)],[1,(c-a-sqrt((c-a)^2+4*b^2))/(2*b)])$ L.M(a,b,c).invert(L); ratsimp(%);
により
と対角化できることがわかります。
ここで固有ベクトル を規格化した
をとります。このとき、行列
を使っても の場合と同じように行列
を対角化することができます:
gp:(c-a+sqrt((c-a)^2+4*b^2))/(2*b)$ gm:(c-a-sqrt((c-a)^2+4*b^2))/(2*b)$ R:matrix([1/sqrt(1+gp^2),gp/sqrt(1+gp^2)],[1/sqrt(1+gm^2),gm/sqrt(1+gm^2)])$ R.M(a,b,c).invert(R); ratsimp(%);
ポイントは
R.transpose(R); ratsimp(%); transpose(R).R; ratsimp(%);
によってわかるように、行列 が直交行列(
)であることです。
すなわち
が成り立ちます。
そこで新しい変数 を
によって導入すると、2次式 を
と表すことができ、さらに
とすると、2次式が新たな変数 を使って
という 、
についての2次式の和の形に書き直すことができます。
あとは 、
についてそれぞれ平方完成し、再度適当に変数変換すると
の形まで変形できます。ここで
です(ただし と仮定しました)。
最後に2次式全体を適当に定数倍することで円錐曲線の標準形が得られます。
円錐曲線(二次曲線)の図示
例1
具体例として
とした場合で の値を変えていって曲線がどのように変化してくか観察してみましょう。
このとき対応する行列式は
により、対応する曲線が変わる臨界値は であるはずです。
P(b):=x^2+2*b*x*y+y^2-1$ load(implicit_plot)$ implicit_plot (P(-4) = 0, [x, -1.5, 1.5], [y, -1.5, 1.5])$
などと入力して
の場合で円錐曲線を描いたものが以下の図です:
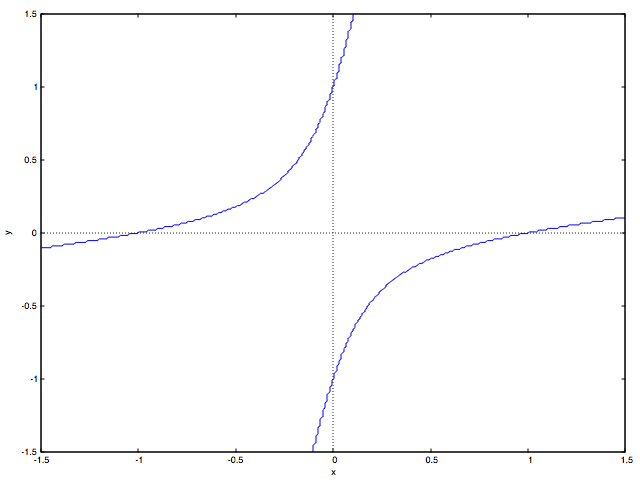
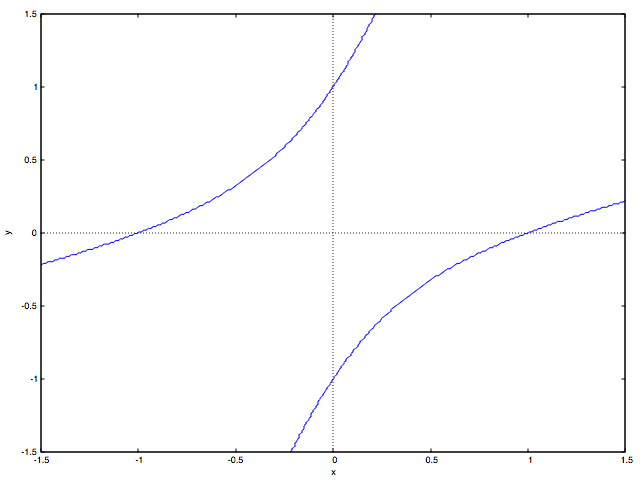
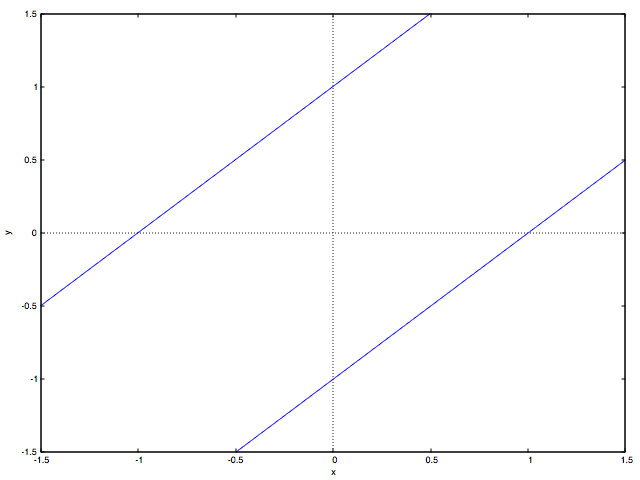


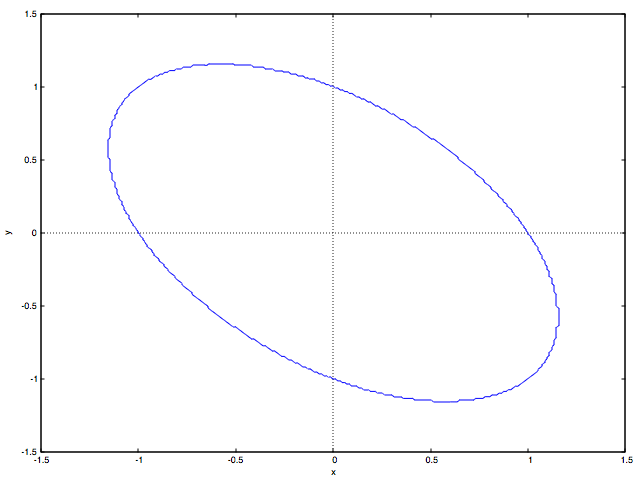
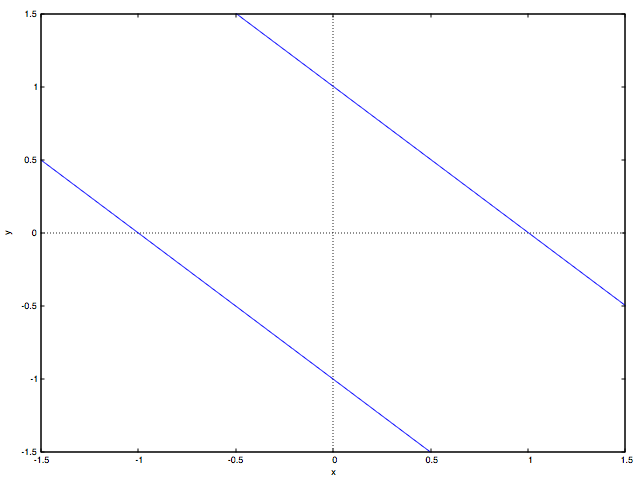


kill(all)$ P(b):=x^2+2*b*x*y+y^2-1$ load(implicit_plot)$ for i:0 step 1 thru 200 do( b:concat("保存ディレクトリ/ファイル名", i, ".eps"), t : float(-5.0 +0.05*i), implicit_plot (P(t) = 0, [x, -2.0, 2.0], [y, -2.0, 2.0], [plot_format, gnuplot], [gnuplot_term, ps], [gnuplot_out_file, b]));
と入力し、 から
刻みに
まで値を変化させた eps ファイルを作成し、
ImageMagick をインストールしたうえでファイルの保存ディレクトリに移動し、ターミナルで
$ convert -dispose previous -layers optimize -loop 0 -delay 5 *.eps anim.gif
と入力することで、GIFアニメを作成したものが次のものです:

双曲線から2つの平行線(これは放物線の極限形とみなす?)、楕円、正円からふたたび楕円、
2つの平行線をへて双曲線へと連続的に曲線の形が変わっていく様子がわかると思います。
例2
別な具体例として
とした場合で の値を変えていって曲線がどのように変化してくか観察してみましょう。
このとき対応する行列式は
により、対応する曲線が変わる臨界値は であるはずです。
kill(all)$ P(a):=a*x^2+y^2+2*x-1$ load(implicit_plot)$ for i:0 step 1 thru 200 do( b:concat("保存ディレクトリ/ファイル名", i, ".eps"), t : float(-5.0 +0.05*i), implicit_plot (P(t) = 0, [x, -2.0, 2.0], [y, -2.0, 2.0], [plot_format, gnuplot], [gnuplot_term, ps], [gnuplot_out_file, b]));
と入力し、上と同様にして から
までの変化をGIFアニメにしたものが次です:

でのスナップショットが次の図です:
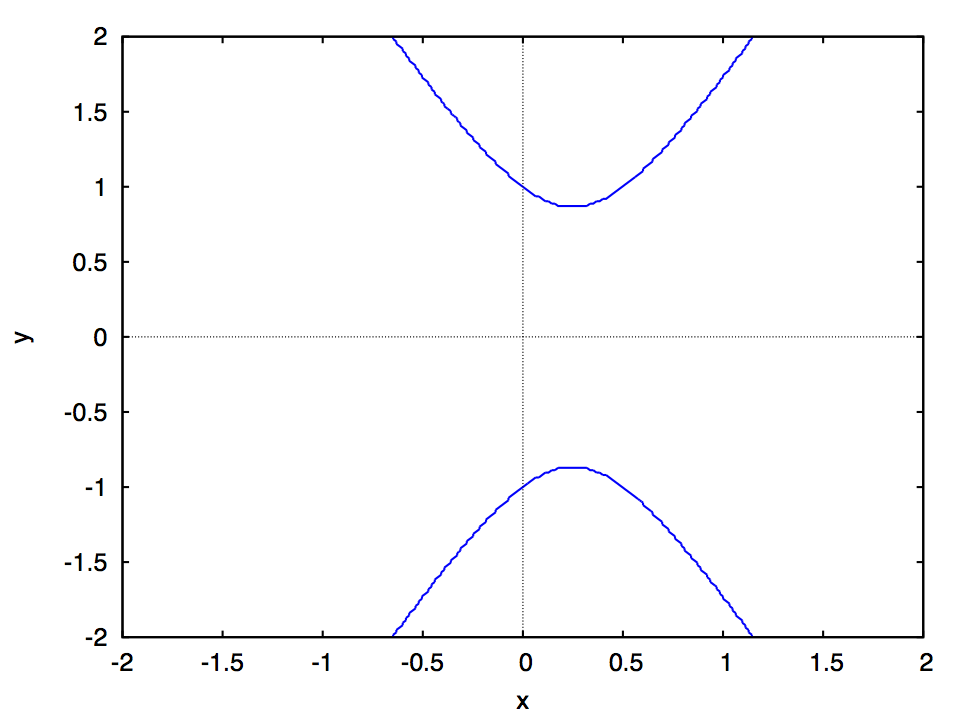
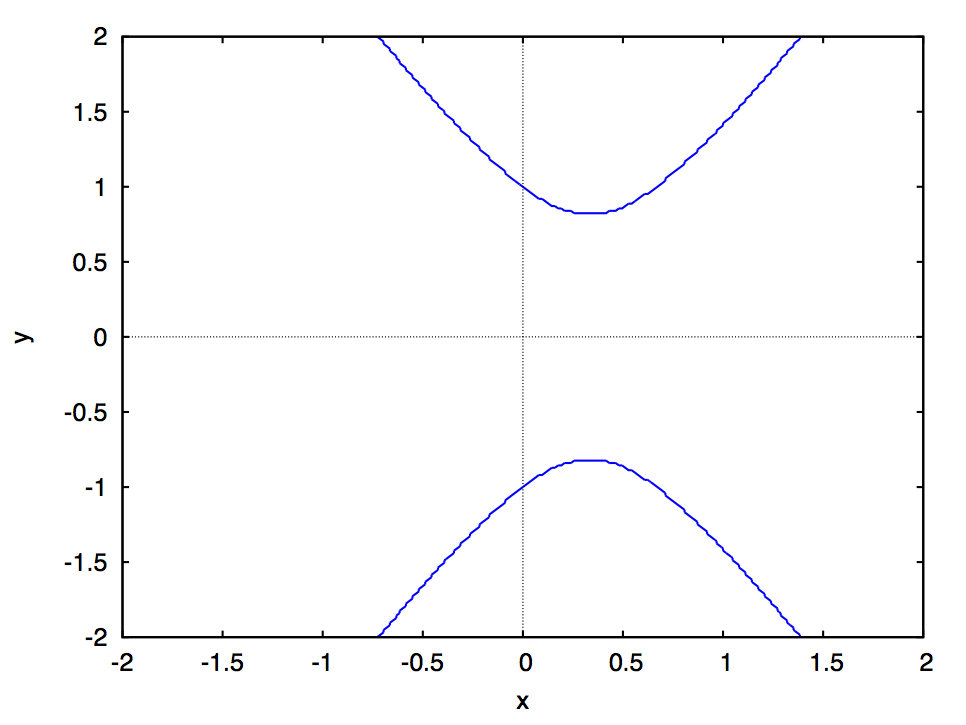
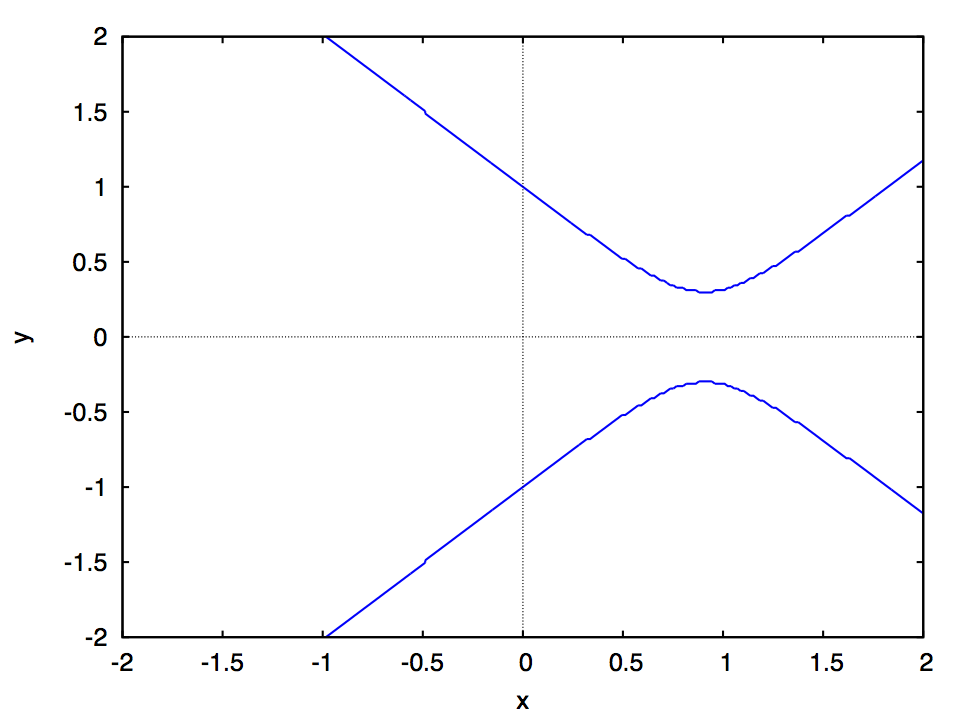
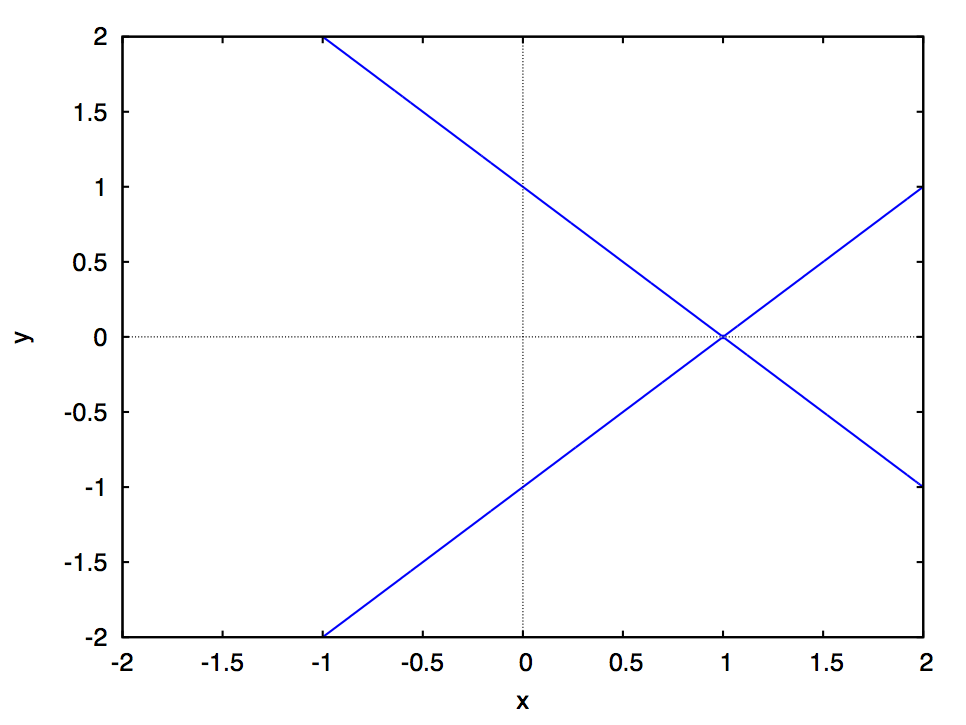
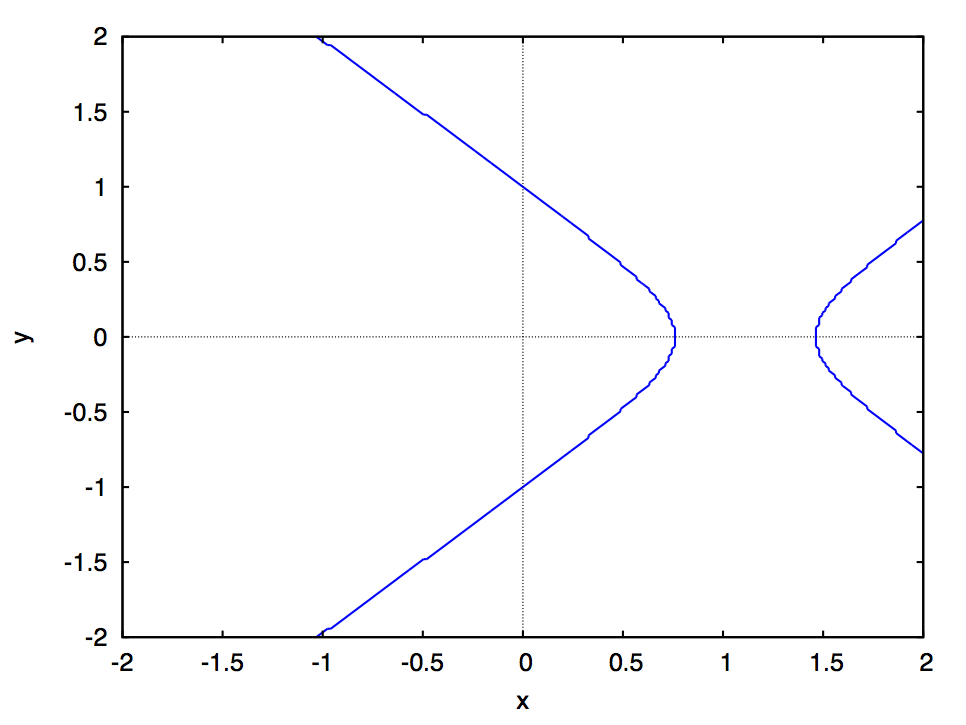

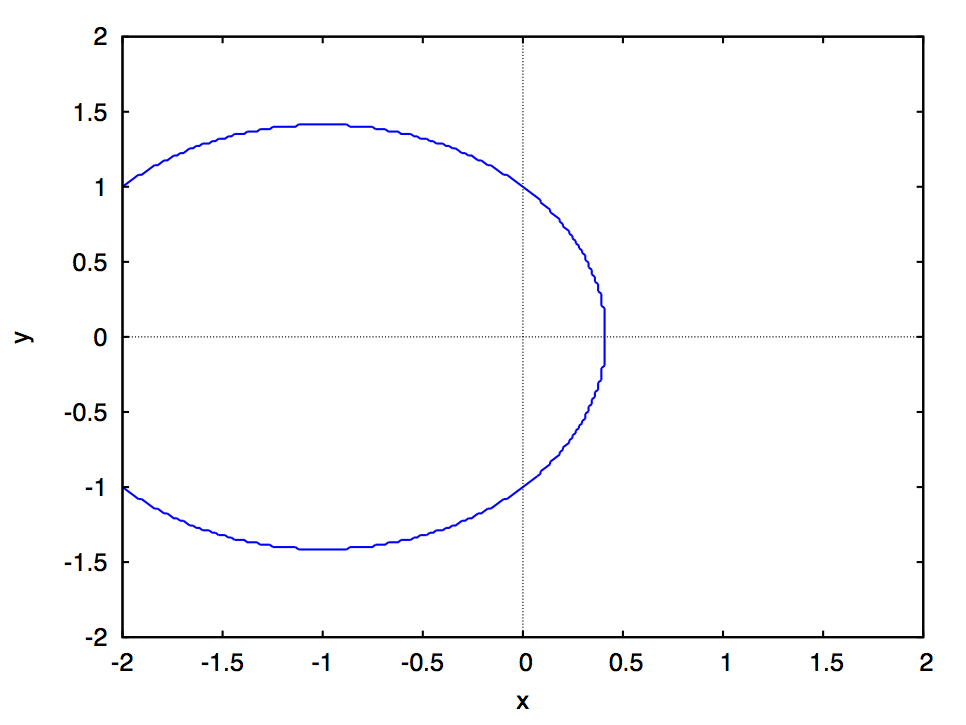
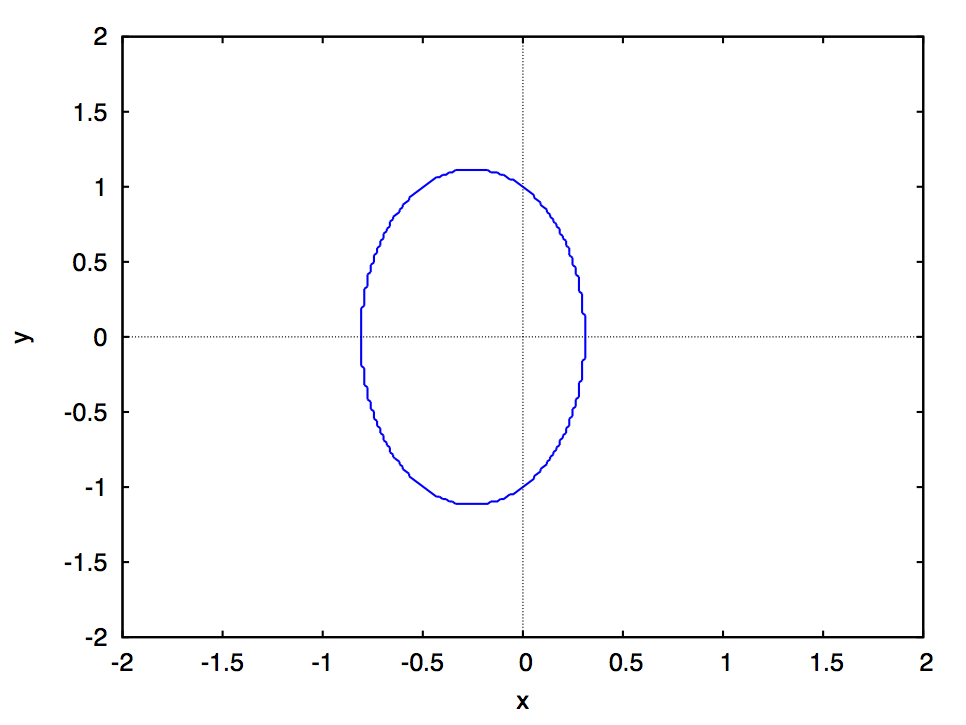
双曲線、二直線(退化した円錐曲線)、双曲線、放物線、楕円と形を変えているのがわかります。
とくに (放物線に対応)が双曲線から楕円に変わる臨界値であることは上で述べた通りですが、
そのほかに も特徴的で、対応する曲線は2つの交差する直線になっています。
これは2次式が
とまとめられるために生じたものです。
具体的には、 に対応する曲線は
となります。
本記事で特に断りなく利用したMaximaでの行列の取り扱いについては過去記事
グラフの描画やGIFアニメ化については
や
が参考になるかと思います。
キーワード:円錐曲線(二次曲線)、行列、Maxima、グラフ描画