機械学習の具体的な問題にPythonを使って、機械学習もPythonも同時に学んでしまいましょう。今回は機械学習の基本的な予測モデルである線形回帰についてまとめました。
この記事では scikit-learn(sklearn)ライブラリを用います。適宜
pip install scikit-learn
などによってダウンロード・インストールしてください。
線形回帰モデルの実装
線形回帰モデルは、入力値 に対して予測値
を線形関数
によってモデル化するものです。問題としては、与えられたデータセットからパラメタ と
の妥当な値を求めるということになります。
from sklearn.linear_model import LinearRegression import numpy as np # サンプルデータ(特徴量Xとターゲットy) X = np.array([[1], [2], [3], [4], [5]]) # 入力(特徴量)データ y = np.array([9.8, 20.1, 28.7, 40.8, 50.2]) # 出力(ターゲット)データ # モデルの作成と学習 model = LinearRegression() model.fit(X, y) # 予測 x_pred = np.array([[2.5], [3.5], [4.5]]) y_pred = model.predict(x_pred) # 結果表示 print("回帰係数(a):", model.coef_[0]) print("切片(b):", model.intercept_) print("予測値:", y_pred)
回帰係数(a): 10.15 切片(b): -0.5299999999999976 予測値: [24.845 34.995 45.145]
ポイント
- model.fit(X, y) でデータを学習
- model.coef_ で傾き a、model.intercept_ で切片 b を取得
- model.predict(X) で予測値を計算
線形回帰モデルの可視化
上で扱ったデータセットと、そこから得られた線形回帰モデルを Matplotlib を使って可視化してみます。
import numpy as np import matplotlib.pyplot as plt from sklearn.linear_model import LinearRegression # サンプルデータ X = np.array([[1], [2], [3], [4], [5]]) # 特徴量 y = np.array([9.8, 20.1, 28.7, 40.8, 50.2]) # 出力データ # モデルの作成と学習 model = LinearRegression() model.fit(X, y) # グラフ描画 plt.scatter(X, y, color="blue", label="Data") # 実際のデータ点 plt.plot(X, y_pred, color="red", linewidth=2, label="Linear Regression") # 予測直線 # タイトルとラベル plt.title("Visualization of Linear Regression") plt.xlabel("Feature") plt.ylabel("Target") plt.legend() plt.show()
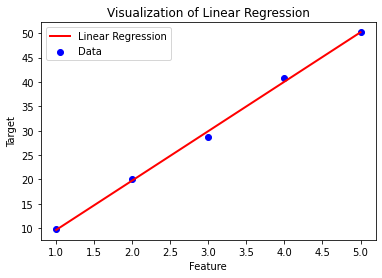
ポイント
- plt.scatter(X, y) で元データを青い点で描画
- plt.plot(X, y_pred) で回帰直線を赤線で描画