Pythonで学ぶ機械学習：主成分分析

機械学習の具体的な問題にPythonを使って、機械学習もPythonも同時に学んでしまいましょう。今回は主成分分析についてまとめました。機械学習では、特徴量が多すぎると計算コストが増えたり、過学習を起こしやすくなったりします。そこで PCA（Principal Component Analysis：主成分分析）を使って、重要な情報を保持しながらデータの次元を削減する方法を学びます。

この記事では scikit-learn（sklearn）ライブラリを用います。適宜

pip install scikit-learn

などによってダウンロード・インストールしてください。

PCAの実装

PCAでは、データの分散が最大になる方向を主成分として抽出し、高次元のデータを低次元（2次元や3次元など）に圧縮します。この手法は、画像圧縮や可視化にも使われます。実装は以下の通りです：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris

# データセット（Irisデータ）
data = load_iris()
X = data.data  # 4次元の特徴量
y = data.target  # クラス（0, 1, 2）

# PCAで2次元に圧縮
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)

# グラフ描画
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, cmap='viridis', edgecolors='k')
plt.xlabel("Principal Component 1")
plt.ylabel("Principal Component 2")
plt.title("PCA Reductioin (Iris data)")
plt.colorbar(label="Class")
plt.show()

ポイント

• PCA(n_components=2) で2次元に圧縮
• pca.fit_transform(X) でデータを変換
• 2次元に削減することでデータの構造を可視化できる

PCAの累積寄与率の確認

PCAでは、どれくらいの情報を保持できているかを確認することが重要です。これを累積寄与率（Explained Variance Ratio）を使って確認します。累積寄与率とは、各主成分がデータの情報をどれだけ保持しているかを表す割合で、累積寄与率が90%以上なら十分な情報を保持できていると考えられます。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris

# データセット（Irisデータ）
data = load_iris()
X = data.data  # 4次元の特徴量

# PCA（すべての主成分を計算）
pca = PCA()
pca.fit(X)

# 寄与率（各主成分の情報量）を取得
explained_variance_ratio = pca.explained_variance_ratio_

# 累積寄与率を計算
cumulative_variance = np.cumsum(explained_variance_ratio)

# グラフ描画
plt.plot(range(1, len(cumulative_variance) + 1),
         cumulative_variance,
         marker='o',
         linestyle='--')
plt.xlabel("Number of PC")
plt.ylabel("EVR")
plt.title("PCA EVR")
plt.grid(True)
plt.show()

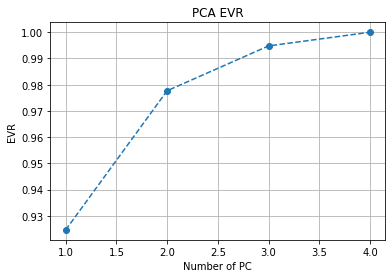
ポイント

• pca.explained_variance_ratio_ で各主成分の寄与率を取得
• np.cumsum() で累積寄与率を計算
• 累積寄与率が90%を超える最小の主成分数を確認すると、適切な次元数がわかる

キーワード：機械学習、Python、基礎