Maximaで方程式・連立方程式を解く、数列を求める

数学の具体的な計算にMaximaを使って、数学もMaximaも同時に学んでしまいましょう。

今回はMaximaを使って方程式・連立方程式を解いてみたいと思います。

厳密に代数的に解く方法、数値的に解く方法、グラフを描画して解く方法をみていきます。

また、漸化式から定まる数列について、その各項を求める方法もみていきます。

Maximaのごく基本的な使い方については以下の記事を参照してください：

pianofisica.hatenablog.com

代数方程式
連立１次方程式
連立方程式
方程式の数値解（Newton法）
漸化式
微分方程式

代数方程式

多項式（変数と定数について有限回の和と積をとったもの）同士を等号で結んだ方程式を

代数方程式といいます。代数方程式の解として表される数を代数的数といいます。

したがって整数、有理数、そして $\sqrt{2}$ などの無理数は代数的数です。

代数的数でない数は超越数と呼ばれます。

同様に、代数的でない方程式のことも超越方程式と呼ばれます。

超越方程式の例としては

$1-\log x=0 \qquad \sin x=0$

などがあげられます。

これらの方程式の解となるNapier数（自然対数の底） $e$ 、円周率 $\pi$ は超越数です。

以下では代数方程式をMaximaを使って解く方法をみていきます。

１次方程式

$ax+b=0$

をMaximaで解くには

solve( a*x+b=0, x );

と入力します。すると解

$\displaystyle{x=-\frac{b}{a}}$

が出力されます。

２次方程式

$ax^2+bx+c=0$

をMaximaで解くには

solve( a*x^2+b*x+c=0, x );

と入力します。解として

$\displaystyle{x={-b-{\sqrt{b^2-4ac}}\over{2a}} ,\qquad x={-b+{\sqrt{b^2-4ac}}\over{2a}}}$

が出力されます。高校数学でもおなじみの公式です。

３次方程式

$ax^3+bx^2+cx+d=0$

をMaximaで解くには

solve( a*x^3+b*x^2+c*x+d=0, x );

と入力します。すると、解

$\displaystyle{x=r^{1/3}-\frac{s}{r^{1/3}}-\frac{b}{3a},\qquad x=\left(\frac{-1\mp i\sqrt{3}}{2}\right)r^{1/3}-\left(\frac{-1\pm i\sqrt{3}}{2}\right)\frac{s}{r^{1/3}}-\frac{b}{3a}\\ r={{\left(27a^2d^2+\left(4b^3-18abc\right)d+4ac^3-b^2c^2\right)^{1/2}}\over{2\,3^{3/2}a^2}}+{{{{bc}}-{{3ad}}}\over{6a^2}}-{{b^3}\over{27a^3}} \\ s=-\frac{b^2}{9a^2}+\frac{c}{3a} }$

が求まります。これが３次方程式の解の公式、ということになるのですが、

公式に目を凝らすと、意味ありげな複素数

$\displaystyle{\frac{-1\pm i\sqrt{3}}{2}}$

に気がつきます。複合の正のほうを便宜上 $\omega$ と呼ぶことにします。すると

omega: (-1+%i*sqrt(3))/2$
expand(omega^2);
expand(omega^3);

により

$\omega^2=\omega^* \quad(\text{$\omega^*$ は $\omega$ の複素共役})$

であり、また $\omega$ は１の３乗根であることがわかります。

このことは、指数関数と三角関数の関係式

$\displaystyle{e^{i\theta}=\cos\theta+i\sin\theta}$

より

$\displaystyle{\omega=\frac{-1+ i\sqrt{3}}{2}=\cos\frac{2\pi}{3}+i\sin\frac{2\pi}{3}=e^{i\frac{2\pi}{3}}}$

であることからもわかります：

polarform((-1+%i*sqrt(3))/2);

３次方程式の解の公式に１の３乗根が現れる理由というのは、掘り下げていくと、実は、

『Galois（ガロア）理論』という数学の分野にも繋がっていくお話（らしいの）ですが、

本記事内に書くのは適切でないのと、知識不足なこともあって、いずれ別記事で書きたいと思います。

ちなみに、Galois理論によると、一般の５次以上の方程式は代数的に解くことができない

（つまり、解の公式が存在しない）ということが証明されます。

４次方程式

$ax^4+bx^3+cx^2+dx+e=0$

をMaximaで解くには

solve( a*x^4+b*x^3+c*x^2+d*x+e=0, x );

と入力すればよいのですが、さすがに一般形は複雑で

$\text{Expression longer than allowed by the configuration setting!}$

という出力で、結果を表示してくれません。

そこで

Sol4(a,b,c,d,e):=solve( a*x^4+b*x^3+c*x^2+d*x+e=0, x )$

として個別に $a, \ b, \ c, \ d, \ e$ を入力するようにすれば、たとえば

Sol4(1,1,1,1,1);

や

Sol4(1,-2,3,2,1);

などとしてその解を表示してくれます。一応、文字を復活させた

Sol4(1,b,c,1,1);

や

Sol4(1,1,c,d,e);

くらいまでなら結果を表示してくれます（が、いかんせん長いのでここには載せられません）。

ちなみに、 $\displaystyle{x=\xi-\frac{b}{4a}}$ と変数を再定義することにより

expand(subst(xi-b/(4*a), x, a*x^4+b*x^3+c*x^2+d*x+e));

多項式は

$\displaystyle{a\xi^4+\left( c-{{3b^2}\over{8a}} \right)\xi^2+\left( d-{{bc}\over{2a}}+{{b^3}\over{8a^2}} \right)\xi+e-{{bd}\over{4a}}+{{b^2c}\over{16a^2}}-{{3b^4}\over{256a^3}}}$

となり、また $a\neq0$ と仮定して良いことから、４次方程式の解の公式は本質的には

Sol4(1,0,c,d,e);

によって与えられることがわかります。

$n-1$ 次の係数が消去できるという同様の議論は一般の $n$ 次式の場合にも成り立ちます。

５次方程式

$ax^4+bx^3+cx^2+dx+e=0$

は一般に代数的に解けないことが知られています。そこで

Sol5(a,b,c,d,e,f):=solve( a*x^5+b*x^4+c*x^3+d*x^2+e*x+f=0, x )$

とすると

Sol5(1,1,1,1,1,1);

などの特別な場合や、因数分解によって低次の代数方程式に帰着される

Sol5(1,-2,1,-3,2,1);

のような場合を除いて、一般には入力した数式がそのまま出力されます。

連立１次方程式

２変数の場合

２つの変数 $x$ と $y$ に対する連立１次方程式

$ax+by=e \\ cx+dy=f$

をMaximaで解くには

solve( [a*x+b*y=e, c*x+d*y=f], [x,y] );

と入力します。すると解

$\displaystyle{x={{de-bf}\over{ad-bc}} ,\qquad y={{af-ce}\over{ad-bc}}}$

が出力されます。例えば

$2x+y=3 \\ x+3y=4$

に対しては

solve( [2*x+y=3, x+3*y=4], [x,y] );

より解

$x=1, \quad y=1$

を得ます。これをグラフを描いて確かめてみましょう：

グラフを描画する（２次元グラフ）

f(x):=rhs(solve(2*x+y=3,y)[1])$
g(x):=rhs(solve(x+3*y=4,y)[1])$
plot2d([f(x),g(x)],[x,-1,2])$

と入力することで
f:id:pianofisica:20190119035636p:plain
という２次元グラフを作成できます。

連立方程式の解は２つの線が交わる点なので、

確かに $x=1, \, y=1$ が解になっていることがわかります。

３変数の場合

同様に、３つの変数 $x$ 、 $y$ 、 $z$ の場合

$ax+by+cz=j \\ dx+ey+fz=k \\ gx+hy+iz=l$

は

solve( [a*x+b*y+c*z=j, d*x+e*y+f*z=k, g*x+h*y+i*z=l], [x,y,z] );

より

$\displaystyle{x={{b\,\left(i\,k-f\,l\right)+c\,\left(e\,l-h\,k\right)+\left(f\,h- e\,i\right)\,j}\over{a\,\left(f\,h-e\,i\right)+b\,\left(d\,i-f\,g \right)+c\,\left(e\,g-d\,h\right)}} \\ y={{-a\,\left(i\,k-f\,l\right)-c\,\left(d\,l-g\,k\right)-\left(f\,g -d\,i\right)\,j}\over{a\,\left(f\,h-e\,i\right)+b\,\left(d\,i-f\,g \right)+c\,\left(e\,g-d\,h\right)}} \\ z={{a\,\left(h\,k-e\,l\right)+b\,\left(d\,l-g\,k\right)+\left(e\,g- d\,h\right)\,j}\over{a\,\left(f\,h-e\,i\right)+b\,\left(d\,i-f\,g \right)+c\,\left(e\,g-d\,h\right)}} }$

と計算されます。例えば

$x+2y+z=0 \\ x+2y+3z=4 \\ 5x+4y+3z=2$

に対しては

solve( [x+2*y+z=0, x+2*y+3*z=4, 5*x+4*y+3*z=2], [x,y,z] );

より、その解は

$x=0, \quad y=-1, \quad z=2$

です。

グラフを描画する（３次元グラフ）

３次元グラフを描画してみましょう：

f(x,y):=rhs(solve(x+2*y+z=0,z)[1])$
g(x,y):=rhs(solve(x+2*y+3*z=4,z)[1])$
h(x,y):=rhs(solve(5*x+4*y+3*z=2,z)[1])$
plot3d([f(x,y),g(x,y),[x,-2,2],[y,-2,2]])$
plot3d([g(x,y),h(x,y),[x,-2,2],[y,-2,2]])$
plot3d([h(x,y),f(x,y),[x,-2,2],[y,-2,2]])$
plot3d([f(x,y),g(x,y),h(x,y),[x,-2,2],[y,-2,2]])$

より、連立された３つの方程式を $z$ について解いて表される曲面を２つずつ選んで描いたものは

また、連立方程式の解は以下のグラフ
f:id:pianofisica:20190119042354p:plain

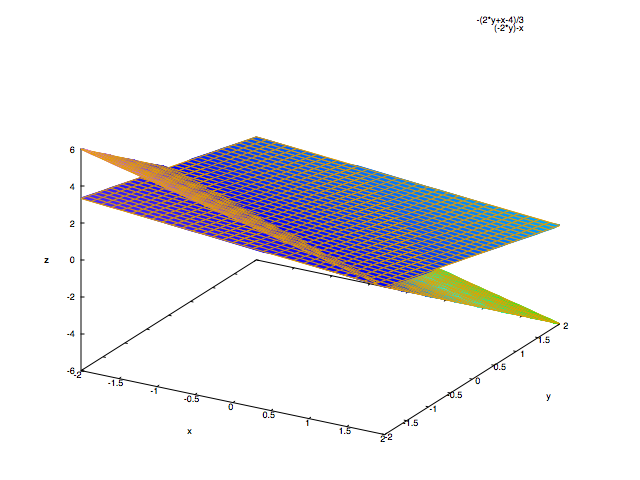
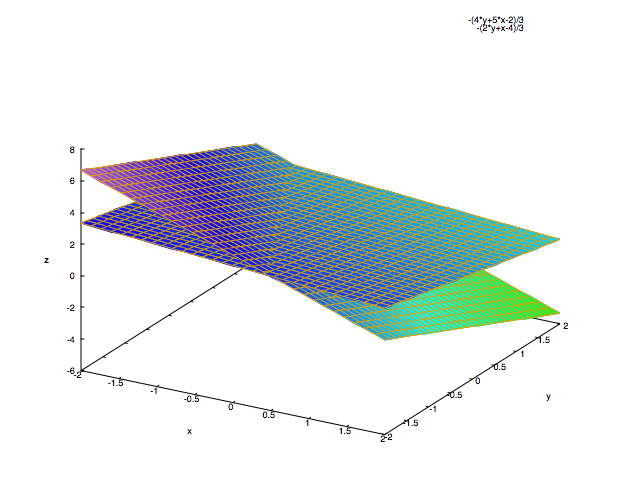
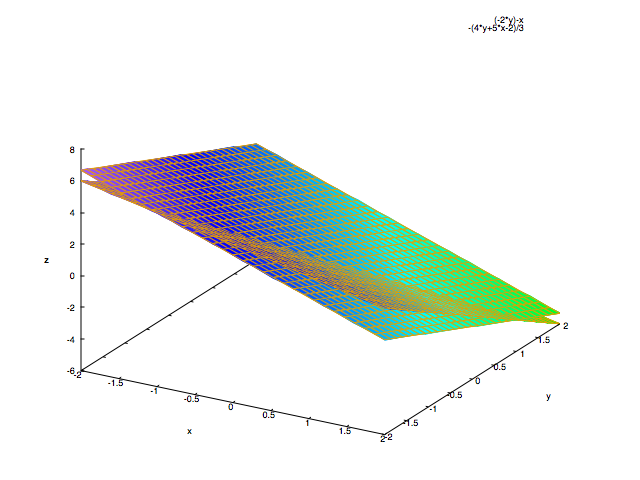
において３つの曲面が交差する点として表されるはずです。

（画像ではわかりづらいですが）グラフを描いて様々な角度から見てみると、

３つの平面が交差する点が確かに $x=0, \, y=-1, \, z=2$ であることがわかります。

連立１次方程式は行列の方程式として表せますが、Maximaでの行列の取り扱いについては

pianofisica.hatenablog.com

を参照してください。

連立方程式

ここまでは１変数の代数方程式、多変数の連立１次方程式についてみてきましたが、

多変数の連立方程式についても

solve( [/*方程式1*/, /*方程式2*/, ...] , [/*変数1*/, /*変数2*/, ...] ])

として解くことができます。

例えば、放物線 $y=ax^2+bx+c$ と直線 $y=gx+h$ の交点は連立方程式

$y=ax^2+bx+c \\ y=gx+h$

の解として求めることができますが、これをMaximaで解くには

solve( [y=a*x^2+b*x+c, y=g*x+h], [x,y] );

と入力します。

同様に、円周 $x^2+y^2=c^2$ と直線 $y=ax+b$ の交点は

solve( [x^2+y^2=c^2, y=a*x+b], [x,y] );

からその答えを知ることができます。

方程式の数値解（Newton法）

これまで、方程式を代数的数として解く方法をみてきましたが、

応用上、数値的に解がわかれば十分という場合もあります。例えば

$x^5+6x^4+x^3+x+1=0$

などはMaximaでは

solve(x^5+6*x^4+x^3+x+1=0, x);

としてわかるように、代数的操作だけでは解を求められず、数式がそのまま出力されてしまいます。

組み込み mnewton を使って数値解を求める

ここで数値的な解がわかればいいという場合であれば、

MaximaにはNewton法が実装されていて、その数値解を求めることができます：

load("mnewton")$ /* mnewtonを使うためにパッケージ"mnewton"を読み込んでおく必要があります */
mnewton(x^5+6*x^4+x^3+x+1=0, x , 0.0);

により数値解

$x=-5.824107105503423$

が求まります。一応確認してみると

subst( -5.824107105503423, x, x^5+6*x^4+x^3+x+1);

から方程式の左辺が数値的には

$-9.094947\dots\times 10^{-13}$

となることから解になっていることがわかります。

Newton法の実装mnewtonの使い方は

mnewton(
[/*方程式1*/, /*方程式2*/, ...] , 
[/*変数1*/, /*変数2*/, ...] , 
[/*変数1の初期値*/, /*変数2の初期値*/, ...] ]);

です。

グラフを使って解を求める（組み込み find_root を使う）

グラフを描画して

plot2d(x^5+6*x^4+x^3+x+1, [x, -5.83,-5.82])$

f:id:pianofisica:20190108200404p:plain — y=x^5+6*x^4+x^3+x+1

によって

$-5.83 < x < -5.82$

の範囲内に解があることがわかります。このようなとき

find_root(x^5+6*x^4+x^3+x+1,-5.83,-5.82);

と入力することによって数値解

$x=-5.824107105503421$

を見つけることができます。

find_root はパッケージを読み込むことが不要で、

求めたい解のある位置が大体わかっている場合に数値解を求めるときにはお手軽です。

しかし

find_root(x^2-2,-2,2);
find_root(x^2-2,-2,0);

としてわかるように、設定した範囲内に複数の根があった場合エラーとなってしまいます。

組み込み allroots 使って数値解を求める

また別な数値解を求める方法として、allroots という実装もあります：

allroots(x^5+6*x^4+x^3+x+1=0);

と入力すると、５つの数値解

$x_1=-5.824107105503422 \\ x_2 =0.4208410439238929 +0.5254096115677801\, i \\ x_3= 0.4208410439238929-0.5254096115677801\,i \\ x_4=-0.508787491172182+0.3464511851389064\,i \\x_5=-0.508787491172182-0.3464511851389064\,i$

が一挙に求められます。

漸化式

$F_{n+2}=F_{n+1}+F_n \qquad F_0=0 \qquad F_1 =1$

のような漸化式から定まる数列について、その各項をMaximaで求めることができます：

F[n]:=F[n-1]+F[n-2]$
F[0]: 0$
F[1]: 1$
makelist(F[n], n, 0, 10);

より数列は

$0, ~1, ~1, ~2, ~3, ~5, ~8, ~13, ~21, ~34, ~55, ~\dots$

と求まります。

ちなみに、この漸化式によって定まる数列をFibonacci（フィボナッチ）数列といいます。

整数列が与えられたとき、その数列がどのような式で表されるのか知りたいときに便利なWebページ

The On-Line Encyclopedia of Integer Sequences® (OEIS®)

を紹介しておきます。数列の一部分を取り出して検索バーに順番通りに入力して検索すると、

データベースと照合して、その数列の他の項や一般式、漸化式などの候補を示してくれます。

試しに、上で求めた数列をコピー＆ペーストして検索するとFibonacci数の説明が出てきます：

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 - OEIS

本記事と同様の内容をプログラミング言語 Pythonで実演しているのが次の記事です：

pianofisica.hatenablog.com

Maximaとの違いを見比べてみるのも面白いかもしれません。

微分方程式

Maximaで微分方程式を解く方法を解説しているのが次の記事です：

pianofisica.hatenablog.com

キーワード：Maxima、gnuplot、方程式、代数方程式、連立方程式、漸化式、グラフ